题目内容
已知函数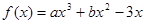 在
在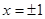 处取得极值,过点
处取得极值,过点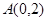 作曲线
作曲线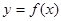 的切线
的切线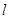 ,(1)求此切线
,(1)求此切线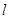 的方程.(2)求切线
的方程.(2)求切线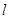 与函数
与函数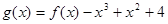 的图象围成的平面图形的面积。
的图象围成的平面图形的面积。
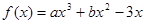 在
在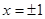 处取得极值,过点
处取得极值,过点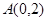 作曲线
作曲线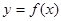 的切线
的切线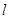 ,(1)求此切线
,(1)求此切线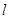 的方程.(2)求切线
的方程.(2)求切线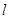 与函数
与函数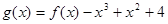 的图象围成的平面图形的面积。
的图象围成的平面图形的面积。(1)y=2;(2)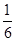 .
.
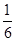 .
.本试题主要是考查了导数在研究函数中的运用。
解:(1)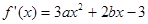 ,依题意,
,依题意,
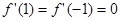 ,即
,即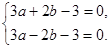 解得
解得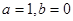
∴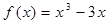 ,
,
曲线方程为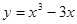 ,点
,点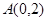 不在曲线上。
不在曲线上。
设切点为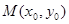 ,则
,则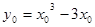
由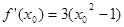 知,切线方程为
知,切线方程为
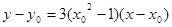
又点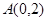 在切线上,有
在切线上,有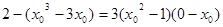
化简得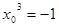 ,解得
,解得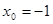
所以切点为 ,切线方程为y=2
,切线方程为y=2
(2)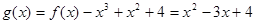
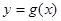 与y=2的交点为(1,2)和(2,2)
与y=2的交点为(1,2)和(2,2)
切线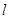 与函数g(x)的图象围成的图形面积为:
与函数g(x)的图象围成的图形面积为:
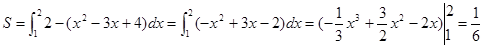
解:(1)
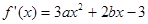 ,依题意,
,依题意,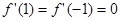 ,即
,即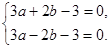 解得
解得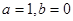
∴
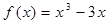 ,
,曲线方程为
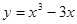 ,点
,点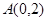 不在曲线上。
不在曲线上。设切点为
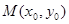 ,则
,则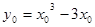
由
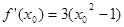 知,切线方程为
知,切线方程为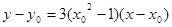
又点
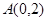 在切线上,有
在切线上,有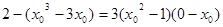
化简得
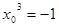 ,解得
,解得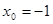
所以切点为
 ,切线方程为y=2
,切线方程为y=2(2)
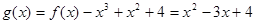
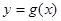 与y=2的交点为(1,2)和(2,2)
与y=2的交点为(1,2)和(2,2)切线
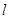 与函数g(x)的图象围成的图形面积为:
与函数g(x)的图象围成的图形面积为: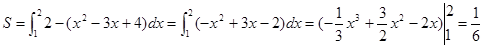

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
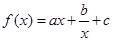 (
(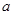 >0)的图象在点
>0)的图象在点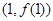 处的切线方程为
处的切线方程为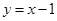 .
.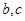 ;
;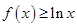 在
在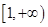 上恒成立,求
上恒成立,求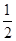 +
+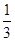 +…+
+…+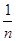 >
>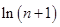 +
+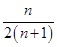
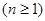 .
.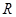 上的可导函数
上的可导函数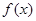 ,当
,当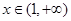 时,
时,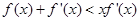 恒成立,
恒成立,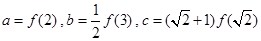 ,则
,则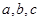 的大小关系为 ( )
的大小关系为 ( )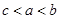

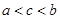
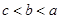

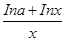 在[1,+∞)上为减函数,求实数a的取值范围.
在[1,+∞)上为减函数,求实数a的取值范围.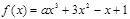 在
在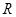 上为减函数,则实数
上为减函数,则实数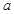 的取值范围是( )
的取值范围是( )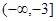
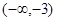
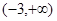
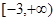
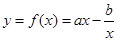 在点
在点 处的切线方程为
处的切线方程为 ,则
,则 的值为 ( )
的值为 ( ) 



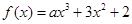 ,若
,若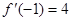 , 则实数
, 则实数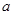 的值等于
的值等于


