题目内容
20. 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )| A. | $\frac{π}{12}$ | B. | $1-\frac{π}{12}$ | C. | $1-\frac{π}{3}$ | D. | 1-$\frac{π}{6}$ |
分析 由已知中的三视图,可知该几何体是一个正方体挖去一个圆锥所得的几何体,分别柱体体积和锥体体积,相减可得答案.
解答 解:由已知中的三视图,可知该几何体是一个正方体挖去一个圆锥所得的几何体,
正方体的体积V=1×1×1=1,
圆锥的底面直径为1,故底面面积为$π×(\frac{1}{2})^{2}$=$\frac{π}{4}$,
高为1,故体积为:$\frac{1}{3}$×$\frac{π}{4}$×1=$\frac{π}{12}$,
故组合体的体积V=1-$\frac{π}{12}$,
故选:B.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
11.动圆过点(0,1),且与直线y=-1相切,则动圆圆心的轨迹是( )
| A. | 直线 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
11.为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费计算电费,每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分按每度0.5元计算.
(1)设月用电量x时,应交电费y元,写出y与x的函数关系式;
(2)小明第一季度的电费情况如下:
则小明家第一季度共用点多少度?
(1)设月用电量x时,应交电费y元,写出y与x的函数关系式;
(2)小明第一季度的电费情况如下:
| 月份 | 一月 | 二月 | 三月 | 四月 |
| 交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
8.已知f(x)=sinx+cosx,且f1(x)=f′(x),fn+1(x)=fn′(x)(n∈N*),则f2015(x)=( )
| A. | -sinx-cosx | B. | cosx-sinx | C. | sinx-cosx | D. | sinx+cosx |
5.已知某四棱锥的三视图(单位:cm)如图所示,则该四棱锥的体积是( )


| A. | $\frac{{\sqrt{3}}}{3}c{m^3}$ | B. | $\frac{{4\sqrt{3}}}{3}c{m^3}$ | C. | $\frac{{8\sqrt{3}}}{3}c{m^3}$ | D. | $\sqrt{3}c{m^3}$ |
12.直线l过点(2,3)且与直线m:3x+2y-4=0垂直,则直线l的方程为( )
| A. | 3x+2y-12=0 | B. | 2x+3y-13=0 | C. | 3x-2y=0 | D. | 2x-3y+5=0 |
9.用火柴棒摆“金鱼”,如图所示:
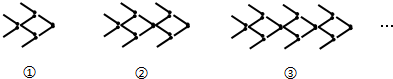
按照上面的规律,第10个“金鱼”图需要火柴棒的根数为( )

按照上面的规律,第10个“金鱼”图需要火柴棒的根数为( )
| A. | 58 | B. | 78 | C. | 62 | D. | 82 |