题目内容
15.已知直线l:5x+2y+3=0.(1)求直线:5x+2y-1=0与直线l的距离;
(2)求直线l2:3x+7y-13=0与直线l的夹角的大小.
分析 (1)利用平行线之间的距离公式求解即可.
(2)直接利用两条直线的夹角个数求解即可.
解答 解:(1)因为l1∥l,所以l1与l的距离为$\frac{|3-(-1)|}{{\sqrt{{5^2}+{2^2}}}}=\frac{{4\sqrt{29}}}{29}$;…(3分)
(2)直线l2与直线l的夹角的余弦值为$cosθ=\frac{|5×3+2×7|}{{\sqrt{{5^2}+{2^2}}\sqrt{{3^2}+{7^2}}}}=\frac{{\sqrt{2}}}{2}$,
因为$θ∈[{0,\;\frac{π}{2}}]$,所以$θ=\frac{π}{4}$,即直线l2与直线l的夹角的大小为$\frac{π}{4}$.…(6分)
点评 本题考查平行线之间的距离的求法,两条直线的夹角的求法,考查计算能力.

练习册系列答案
相关题目
10.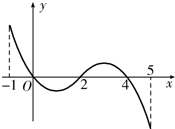 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,
f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数
y=f(x)-a的零点的个数为( )
 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
y=f(x)-a的零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20. 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )
 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )| A. | $\frac{π}{12}$ | B. | $1-\frac{π}{12}$ | C. | $1-\frac{π}{3}$ | D. | 1-$\frac{π}{6}$ |
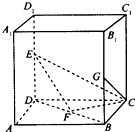 如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.