��Ŀ����
11��Ϊ���ٿ�����Ⱦ��ij�й��������õ磨����ȼ����ȼú�������÷ֶμƷѼ����ѣ�ÿ���õ粻����100��ʱ����ÿ��0.57Ԫ���㣬ÿ���õ�������100��ʱ�����е�100����ԭ���շѣ������IJ��ְ�ÿ��0.5Ԫ���㣮��1�������õ���xʱ��Ӧ�����yԪ��д��y��x�ĺ�����ϵʽ��
��2��С����һ���ȵĵ��������£�
| �·� | һ�� | ���� | ���� | ���� |
| ���ѽ�� | 76Ԫ | 63Ԫ | 45.6Ԫ | 184.6Ԫ |
���� ��1������Ӧ�����=���õ������ÿ�ȵ�ѽ���������ϵ����Ϊÿ�ȵ�ѱ���һ������Ҫ�������ۣ�
��2���ֱ����ÿ��������ѣ����ÿ�����õ�Ķ���������ཻ�����������
��� �⣺��1����0��x��100ʱ��y=0.57x��
��x��100ʱ��y=0.5����x-100��+0.57��100=0.5x-50+57=0.5x+7��
����������ʽΪy=$\left\{\begin{array}{l}0.57x��0��x��100\\ 0.5x+7��x��100\end{array}\right.$--��6�֣�
��2�������⣬
һ�·ݣ�0.5x+7=76����x=138���ȣ���
���·ݣ�0.5x+7=63����x=112���ȣ���
���·ݣ�0.57x=45.6����x=80���ȣ���
���Ե�һ���ȹ��õ磺
138+112+80=330���ȣ���
��С���ҵ�һ���ȹ��õ�330�ȣ�--��12�֣�
���� ������Ҫ�����˺���ģ�͵�ѡ����Ӧ�ã��Լ����ݺ���ֵ���Ա��������ڻ�����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
20����֪����x��y�����ϵy=0.1x-10������z��y����أ������н�������ȷ���ǣ�������
| A�� | x��y����أ�x��z����� | B�� | x��y����أ�x��z����� | ||
| C�� | x��y����أ�x��z����� | D�� | x��y����أ�x��z����� |
16������$P��-\sqrt{3}��-1��$��ֱ��l��Բx2+y2=1��������ͬ�Ĺ����㣬��ֱ��l��б�ʵ�ȡֵ��Χ�ǣ�������
| A�� | $��0��\frac{{\sqrt{3}}}{3}��$ | B�� | $[0��\sqrt{3}]$ | C�� | $[\frac{{\sqrt{3}}}{3}��\sqrt{3}��$ | D�� | $��0��\sqrt{3}��$ |
20��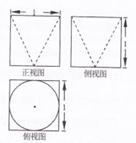 ij�����������ͼ��ͼ��ʾ������������ǣ�������
ij�����������ͼ��ͼ��ʾ������������ǣ�������
 ij�����������ͼ��ͼ��ʾ������������ǣ�������
ij�����������ͼ��ͼ��ʾ������������ǣ�������| A�� | $\frac{��}{12}$ | B�� | $1-\frac{��}{12}$ | C�� | $1-\frac{��}{3}$ | D�� | 1-$\frac{��}{6}$ |
 ��ͼ���ⳤΪ1��������ABCD-A1B1C1D1��E��F��G�ֱ���DD1��BD��BB1���е㣮
��ͼ���ⳤΪ1��������ABCD-A1B1C1D1��E��F��G�ֱ���DD1��BD��BB1���е㣮