题目内容
9．用火柴棒摆“金鱼”，如图所示：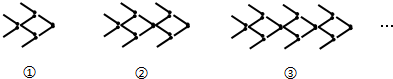
按照上面的规律，第10个“金鱼”图需要火柴棒的根数为（ ）
| A． | 58 | B． | 78 | C． | 62 | D． | 82 |
分析 观察给出的3个例图，注意火柴棒根数的变化是图②的火柴棒比图①的多6根，图③的火柴棒比图②的多6根，而图①的火柴棒的根数为2+6
解答 解：由题意知：图②的火柴棒比图①的多6根，图③的火柴棒比图②的多6根，而图①的火柴棒的根数为2+6，
∴第n条小鱼需要（2+6n）根，
当n=10时，第10个“金鱼”图需要火柴棒的根数为2+6×10=62，
故答案为：62．
点评 本题考查了规律型中的图形变化问题，本题的解答体现了由特殊到一般的数学方法（归纳法），先观察特例，找到火柴棒根数的变化规律，然后猜想第n条小鱼所需要的火柴棒的根数
练习册系列答案
相关题目
20．已知变量x和y满足关系y=0.1x-10，变量z与y负相关，则下列结论中正确的是（ ）
| A． | x与y负相关，x与z负相关 | B． | x与y正相关，x与z正相关 | ||
| C． | x与y正相关，x与z负相关 | D． | x与y负相关，x与z正相关 |
20．
某几何体的三视图如图所示，则它的体积是（ ）
某几何体的三视图如图所示，则它的体积是（ ）| A． | $\frac{π}{12}$ | B． | $1-\frac{π}{12}$ | C． | $1-\frac{π}{3}$ | D． | 1-$\frac{π}{6}$ |
18．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}-2x（x＜0）}\\{\frac{ln（x+1）}{x+1}，（x≥0）}\end{array}\right.$，参数k∈[-1，1]，则方程f（x）-kx-k=0有四个实数根的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2e}$ | D． | $\frac{1}{4e}$ |