题目内容
10.已知tan(π-α)=2.化简下列各式:(1)$\frac{sin(2π-α)+2cos(π-α)}{sin(π-α)+cos(3π+α)}$;
(2)1-2cos2α
分析 利用三角函数的诱导公式分别化简,利用商数关系求值.
解答 解:由已知得到tanα=-2,
所以(1)$\frac{sin(2π-α)+2cos(π-α)}{sin(π-α)+cos(3π+α)}$=$\frac{-sinα-2cosα}{sinα-cosα}$=$\frac{-tanα-2}{tanα-1}$=0;
(2)1-2cos2α=cos2α-sin2α=$\frac{co{s}^{2}α-si{n}^{2}α}{si{n}^{2}α+co{s}^{2}α}$=$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$=$\frac{1-4}{1+4}=-\frac{3}{5}$.
点评 本题考查了三角函数的诱导公式的运用以及对于奇次三角函数式的求值的方法考查.属于基础题.

练习册系列答案
相关题目
20. 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )
 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )| A. | $\frac{π}{12}$ | B. | $1-\frac{π}{12}$ | C. | $1-\frac{π}{3}$ | D. | 1-$\frac{π}{6}$ |
18.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x(x<0)}\\{\frac{ln(x+1)}{x+1},(x≥0)}\end{array}\right.$,参数k∈[-1,1],则方程f(x)-kx-k=0有四个实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2e}$ | D. | $\frac{1}{4e}$ |
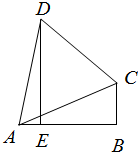 如图,在△ABC中,∠B为直角,DE⊥AB于E,AC⊥DC,设BC=1.
如图,在△ABC中,∠B为直角,DE⊥AB于E,AC⊥DC,设BC=1.