题目内容

8．已知f（x）=sinx+cosx，且f1（x）=f′（x），fn+1（x）=fn′（x）（n∈N*），则f2015（x）=（　　）
A．-sinx-cosxB．cosx-sinxC．sinx-cosxD．sinx+cosx

分析 求函数的导数，确定函数fn（x）的周期性即可．

解答 解：∵f（x）=sinx+cosx，
∴f1（x）=f′（x）=cosx-sinx，
∴f2（x）=f1′（x）=-sinx-cosx，
f3（x）=f2′（x）=-cosx+sinx，
f4（x）=f3′（x）=sinx+cosx，
f5（x）=f4′（x）=cosx-sinx，
…，
fn+4（x）=fn（x），
即fn（x）的周期为4，
f2015（x）=f3（x）=sinx-cosx，
故选：C．

点评 本题主要考查导数的计算，根据导数公式求出函数的周期性是解决本题的关键．

练习册系列答案
相关题目
19．（1）计算$\frac{i-2\sqrt{3}}{1+2\sqrt{3}i}$+（5+i19）-${（\frac{1+i}{\sqrt{2}}）}^{22}$
（2）已知方程x2+ax+b=0（a，b∈R）有一个根是1+2i，求a，b的值．
20．已知变量x和y满足关系y=0.1x-10，变量z与y负相关，则下列结论中正确的是（　　）
A．x与y负相关，x与z负相关B．x与y正相关，x与z正相关
C．x与y正相关，x与z负相关D．x与y负相关，x与z正相关
16．过点$P（-\sqrt{3}，-1）$的直线l与圆x2+y2=1有两个不同的公共点，则直线l的斜率的取值范围是（　　）
A．$（0，\frac{{\sqrt{3}}}{3}）$B．$[0，\sqrt{3}]$C．$[\frac{{\sqrt{3}}}{3}，\sqrt{3}）$D．$（0，\sqrt{3}）$
3．如图，棱长为1的正方体ABCD-A1B1C1D1，E，F，G分别是DD1，BD，BB1的中点．
（1）求证：EF⊥CF；
（2）求$\overrightarrow{EF}$与$\overrightarrow{CG}$所成角的余弦值．
13．已知定点A（4，2）和圆（x+2）2+y2=1上的动点B，则线段AB的中点P的轨迹方程为（x-1）2+（y-1）2=1．
20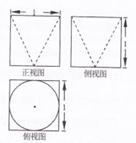．某几何体的三视图如图所示，则它的体积是（　　）
A．$\frac{π}{12}$B．$1-\frac{π}{12}$C．$1-\frac{π}{3}$D．1-$\frac{π}{6}$
17．（1）化简：$\frac{{cos（α+\frac{π}{2}）}}{{sin（\frac{5π}{2}+α）}}•cos（α-π）+\frac{sin（-α）}{tan（α+π）}$；
（2）已知tanα=2，求$\frac{sinα+2cosα}{2sinα-cosα}$的值．
18．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}-2x（x＜0）}\\{\frac{ln（x+1）}{x+1}，（x≥0）}\end{array}\right.$，参数k∈[-1，1]，则方程f（x）-kx-k=0有四个实数根的概率为（　　）
A．$\frac{1}{2}$B．$\frac{1}{4}$C．$\frac{1}{2e}$D．$\frac{1}{4e}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网