题目内容
11.动圆过点(0,1),且与直线y=-1相切,则动圆圆心的轨迹是( )| A. | 直线 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
分析 设出动圆圆心的坐标,根据题意可知圆心到定点P和到直线l的距离都等于半径,进而利用抛物线的定义可得结论.
解答 解:设动圆圆心坐标为(x,y)
∵动圆过定点P(0,1),且与定直线l:y=-1相切,
∴圆心到定点P和到直线l的距离都等于半径,
∴根据抛物线的定义可知动圆圆心的轨迹是抛物线.
故选:D.
点评 本题利用抛物线的定义来求轨迹方程,正确利用抛物线的定义是关键.

练习册系列答案
相关题目
20.已知变量x和y满足关系y=0.1x-10,变量z与y负相关,则下列结论中正确的是( )
| A. | x与y负相关,x与z负相关 | B. | x与y正相关,x与z正相关 | ||
| C. | x与y正相关,x与z负相关 | D. | x与y负相关,x与z正相关 |
20. 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )
 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )| A. | $\frac{π}{12}$ | B. | $1-\frac{π}{12}$ | C. | $1-\frac{π}{3}$ | D. | 1-$\frac{π}{6}$ |
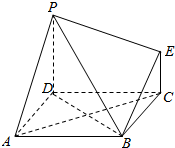 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且