题目内容
10．
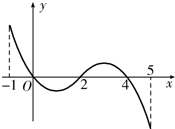已知函数f（x）的定义域为[-1，5]，部分对应值如表，| x | -1 | 0 | 2 | 4 | 5 |
| f（x） | 1 | 2 | 0 | 2 | 1 |
y=f（x）-a的零点的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据导函数图象，画出原函数的草图，利用1＜a＜2，即可得到函数y=f（x）-a的零点的个数
解答 解：由导函数的图象和原函数的关系得，原函数的大致图象如图：
因为f（0）=f（3）=2，1＜a＜2，
所以函数y=f（x）-a的零点的个数为4个．
故选：D．
点评 本题主要考查导函数和原函数的单调性之间的关系．二者之间的关系是：导函数为正，原函数递增；导函数为负，原函数递减，本题属于中档题
练习册系列答案
习题精选系列答案
相关题目
1．函数f（x）=ex-x的单调递增区间是（ ）
| A． | （-∞，1] | B． | [1，+∞） | C． | （-∞，0] | D． | （0，+∞） |
20．已知0＜A＜$\frac{π}{2}$，且cosA=$\frac{2}{3}$，那么sin2A等于（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{7}{9}$ | C． | $\frac{8}{9}$ | D． | $\frac{{4\sqrt{5}}}{9}$ |