题目内容

19．sin40°（tan10°-$\sqrt{3}$）=-1．

分析 首先切化弦，然后通分变形为两角差的正弦公式，逆用化简求值．

解答 解：原式=sin40°（$\frac{sin10°}{cos10°}-\sqrt{3}$）=sin40°$\frac{2（\frac{1}{2}sin10°-\frac{\sqrt{3}}{2}cos10°）}{cos10°}$=2sin40°sin（10°-60°）$\frac{1}{cos10°}$=$\frac{-2sin40°sin50°}{cos10°}$=-$\frac{sin80°}{cos10°}$=-1；
故答案为：-1．

点评 本题考查了三角函数式的化简求值；一般首先切化弦，然后配凑两角差的正弦公式，逆用化简公式求值．

练习册系列答案
相关题目
10．设x，y，z均大于0，则三个数：x+$\frac{1}{y}$，y+$\frac{1}{z}$，z+$\frac{1}{x}$的值（　　）
A．都大于2B．至少有一个不大于2
C．都小于2D．至少有一个不小于2
10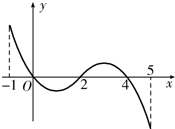．已知函数f（x）的定义域为[-1，5]，部分对应值如表，
x-10245
f（x）12021
f（x）的导函数y=f′（x）的图象如图所示．当1＜a＜2时，函数
y=f（x）-a的零点的个数为（　　）
A．1B．2C．3D．4
7．不论m为何实数，直线mx-y+3=0恒过定点（0，3）（填点的坐标）
14．总体编号为001，002，003，…，299，300的300个个体组成．利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第3、4、5列数字开始由左到右依次选取三个数字，则选出来的第5个个体的编号为（　　）
A．080B．263C．140D．280
4．已知函数f（x）=2-x2-log2x，正实数a、b、c满足f（a）＜f（b）＜0＜f（c），若实数m是方程f（x）=0的一个根，那么下列四个结论：①m＞a；②m＜b；③m＞c；④$m＞\frac{1}{2}（a+b）$．其中成立的是②③．
11．函数 f（x）=2015x2+lnx-x的极值点的个数是（　　）
A．0B．1C．2D．无数个
8．已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1，F2，过右焦点F2作x轴的垂线，交椭圆于A，B两点．若等边△ABF1的周长为$4\sqrt{3}$，则椭圆的方程为（　　）
A．$\frac{x^2}{3}+\frac{y^2}{2}=1$B．$\frac{x^2}{3}+\frac{y^2}{6}=1$C．$\frac{x^2}{2}+\frac{y^2}{3}=1$D．$\frac{x^2}{9}+\frac{y^2}{4}=1$
9．函数y=sin2x+cos2x的值域是（　　）
A．[-1，1]B．[-2，2]C．[-1，$\sqrt{2}$]D．[-$\sqrt{2}$，$\sqrt{2}$]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网