题目内容
18.已知直线l1经过点A(m,1),B(-3,4),l2经过点C(1,m),D(-1,m+1),若l1⊥l2,则m的值为-$\frac{9}{2}$.分析 由已知中l1⊥l2,可知两直线斜率的乘积为-1,结合直线所过的点,求出两直线的斜率,进而构造关于m的方程,可得答案.
解答 解:已知直线l1经过点A(m,1),B(-3,4),
l2经过点C(1,m),D(-1,m+1),
若l1⊥l2,则m≠-3,
故l1的斜率k1=$\frac{-3}{m+3}$,l2的斜率k2=$\frac{1}{-2}$,
由k1•k2=$\frac{-3}{m+3}$×$\frac{1}{-2}$=-1,得:m=-$\frac{9}{2}$,
故答案为:-$\frac{9}{2}$
点评 本题考查的知识点是斜率公式,直线垂直的充要条件,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.设x,y,z均大于0,则三个数:x+$\frac{1}{y}$,y+$\frac{1}{z}$,z+$\frac{1}{x}$的值( )
| A. | 都大于2 | B. | 至少有一个不大于2 | ||
| C. | 都小于2 | D. | 至少有一个不小于2 |
10.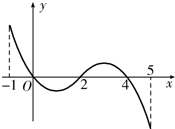 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,
f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数
y=f(x)-a的零点的个数为( )
 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
y=f(x)-a的零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1,F2,过右焦点F2作x轴的垂线,交椭圆于A,B两点.若等边△ABF1的周长为$4\sqrt{3}$,则椭圆的方程为( )
| A. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | B. | $\frac{x^2}{3}+\frac{y^2}{6}=1$ | C. | $\frac{x^2}{2}+\frac{y^2}{3}=1$ | D. | $\frac{x^2}{9}+\frac{y^2}{4}=1$ |
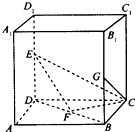 如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.