题目内容
2.已知a>0且a≠1,设命题p:函数$y=lo{{g}_{a}}^{(x+1)}$在x∈(0,+∞)内单调递减,命q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点,若“¬p且q”为真命题,求a的取值范围.分析 根据条件分别求出命题p,q的等价条件,结合复合命题之间的关系进行求解即可.
解答 解:若函数$y=lo{{g}_{a}}^{(x+1)}$在x∈(0,+∞)内单调递减,则0<a<1,即p:0<a<1.
若y=x2+(2a-3)x+1与x轴交于不同的两点,
则判别式△=(2a-3)2-4>0,
解得a>$\frac{5}{2}$或0<a<$\frac{1}{2}$,即q:a>$\frac{5}{2}$或0<a<$\frac{1}{2}$,
若“¬p且q”为真命题,
则¬p,q都为真命题,
即p是假命题,q是真命题,
则$\left\{\begin{array}{l}{a>1}\\{a>\frac{5}{2}或0<a<\frac{1}{2}}\end{array}\right.$,解得a>$\frac{5}{2}$.
点评 本题主要考查复合命题真假之间的关系以及应用,根据条件求出命题p,q的等价条件是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.边长为6的正方形ABCD的中心为O,以O为圆心2为半径作圆,点P是圆O上的任意一点,点Q是边AB,BC,CD,DA上的任意一点(含端点),则$\overrightarrow{PQ}$•$\overrightarrow{DA}$的取值范围为( )
| A. | [-40,40] | B. | [-30,30] | C. | [-15,15] | D. | [-10,10] |
10.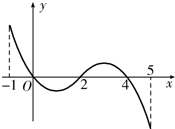 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,
f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数
y=f(x)-a的零点的个数为( )
 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
y=f(x)-a的零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.总体编号为001,002,003,…,299,300的300个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第3、4、5列数字开始由左到右依次选取三个数字,则选出来的第5个个体的编号为( )


| A. | 080 | B. | 263 | C. | 140 | D. | 280 |
11.函数 f(x)=2015x2+lnx-x的极值点的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |