题目内容
1.已知圆C:x2+y2=4和直线l:3x+4y+12=0,点P是圆C上的一动点,直线与坐标轴的交点分别为点A、B,(1)求与圆C相切且平行直线l的直线方程;
(2)求△PAB面积的最大值.
分析 (1)根据题意设所求方程为3x+4y+a=0,根据直线与圆相切时,圆心到直线的距离d=r求出a的值,即可确定出所求直线方程;
(2)当直线与AB平行,且与圆相切时,△PAB面积的最大值,如图所示,求出|AB|与|MN|的长,即可确定出△PAB面积的最大值.
解答 解:(1)设所求直线方程为3x+4y+a=0,
由题意得:圆心(0,0)到直线的距离d=r,即$\frac{|a|}{5}$=2,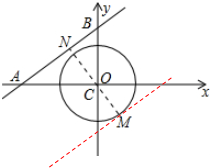
解得:a=±10,
则所求直线方程为3x+4y±10=0;
(2)当直线与AB平行,且与圆相切时,△PAB面积的最大值,
此时直线方程为3x+4y-10=0,
∵点C到直线AB的距离|CN|=$\frac{12}{5}$,CM=2,
∴|MN|=$\frac{12}{5}$+2=$\frac{22}{5}$,
∵A(-4,0),B(0,3),即OA=4,OB=3,
∴|AB|=5,
则△PAB面积最大值为$\frac{1}{2}$×5×$\frac{22}{5}$=11.
点评 此题考查了直线与圆的方程的应用,涉及的知识有:点到直线的距离公式,两直线平行时斜率的关系,以及直线与圆相切的性质,熟练掌握公式及性质是解本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
13.边长为6的正方形ABCD的中心为O,以O为圆心2为半径作圆,点P是圆O上的任意一点,点Q是边AB,BC,CD,DA上的任意一点(含端点),则$\overrightarrow{PQ}$•$\overrightarrow{DA}$的取值范围为( )
| A. | [-40,40] | B. | [-30,30] | C. | [-15,15] | D. | [-10,10] |
10.设x,y,z均大于0,则三个数:x+$\frac{1}{y}$,y+$\frac{1}{z}$,z+$\frac{1}{x}$的值( )
| A. | 都大于2 | B. | 至少有一个不大于2 | ||
| C. | 都小于2 | D. | 至少有一个不小于2 |
17.深圳市某学校为了了解学生使用手机与学习成绩之间的关系,抽查了有手机同学40名,其中成绩为优秀的人数24名,抽查没有手机同学20人,其中成绩为优秀的人数15名,
(1)根据以上数据完成下面的2×2列联表(单位:人)
(2)根据题(1)中表格的数据计算,你有多大的把握,认为学生手机与成绩之间有关系?
(1)根据以上数据完成下面的2×2列联表(单位:人)
| 拥有手机 | 没有手机 | 合计 | |
| 成绩优秀 | |||
| 成绩不优势 | |||
| 合计 |
10. 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,
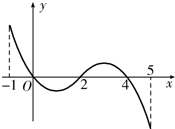
f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数
y=f(x)-a的零点的个数为( )
 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
y=f(x)-a的零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.函数 f(x)=2015x2+lnx-x的极值点的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |