题目内容

1．函数f（x）=ex-x的单调递增区间是（　　）
A．（-∞，1]B．[1，+∞）C．（-∞，0]D．（0，+∞）

分析 先求出函数的导数，由导函数大于0，从而求出函数的递增区间．

解答 解：由f′（x）=ex-1，
令f′（x）＞0，解得：x＞0，
故选：D．

点评 本题考察了函数的单调性，考察导数的应用，是一道基础题．

练习册系列答案
相关题目
11．在平面内，|AB|=4，P，Q满足kAP•kBP=-$\frac{1}{9}$，kAQ•kBQ=-1，且对任意λ∈R，|λ$\overrightarrow{AP}$-$\overrightarrow{AB}$|的最小值为2，则|PQ|的取值范围是[2-$\frac{2\sqrt{3}}{3}$，2+$\frac{2\sqrt{3}}{3}$]．
12．如图，在棱长为1正方体ABCD-A1B1C1D1中，证明：B1D⊥平面ACD1．
9．要制作一个容器为4m3，高为1m的无盖长方形容器，已知该容器的底面造价是每平方米20元，侧面造价是每平方米10元．问：当容器底面如何设计时，使得容器总造价最低，并求出最小值．
16．复数z=$\frac{-2i}{1+i}$的虚部为（　　）
A．1B．-1C．iD．-i
6．定义：分子为1且分母为正整数的分数称为单位分数．我们可以把1分拆为若干个不同的单位分数之和．如：1=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$，1=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{12}$，1=$\frac{1}{2}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$，…
依此类推可得：1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{m}$+$\frac{1}{n}$+$\frac{1}{20}$+$\frac{1}{30}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$
其中m≤n，m，n∈N*，则m+n=23．
13．边长为6的正方形ABCD的中心为O，以O为圆心2为半径作圆，点P是圆O上的任意一点，点Q是边AB，BC，CD，DA上的任意一点（含端点），则$\overrightarrow{PQ}$•$\overrightarrow{DA}$的取值范围为（　　）
A．[-40，40]B．[-30，30]C．[-15，15]D．[-10，10]
10．设x，y，z均大于0，则三个数：x+$\frac{1}{y}$，y+$\frac{1}{z}$，z+$\frac{1}{x}$的值（　　）
A．都大于2B．至少有一个不大于2
C．都小于2D．至少有一个不小于2
10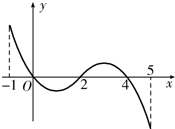．已知函数f（x）的定义域为[-1，5]，部分对应值如表，
x-10245
f（x）12021
f（x）的导函数y=f′（x）的图象如图所示．当1＜a＜2时，函数
y=f（x）-a的零点的个数为（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网