题目内容
5.已知p:关于x的不等式${∫}_{0}^{x}$(2t+1)dt-m>0对任意x∈[1,2]恒成立;q:f(x)=$\left\{\begin{array}{l}{{x}^{2},}&{x≥0}\\{x-1,}&{x<0}\end{array}\right.$,不等式f(m2)>f(m+2)成立.若p∨q为真,p∧q为假,求m的取值范围.分析 先根据定积分求解方法,函数f(x)的单调性求出p,q下的m的取值范围,然后根据p∨q为真,p∧q为假得到p,q一真一假,所以有p真q假,和p假q真两种情况,求出每种情况的m的取值范围再求并集即可
解答 解:p:${∫}_{0}^{x}$(2t+1)dt=(t2+t)|${\;}_{0}^{x}$=x2+x;
∴x2+x-m>0在x∈[1,2]上恒成立;
∴m<x2+x=(x+$\frac{1}{2}$)2-$\frac{1}{4}$对任意x∈[1,2]恒成立;
∴函数x2+x在[1,2]上单调递增,
∴该函数的最小值为2;
∴m<2;
q:由f(x)解析式知函数y=x2在[0,+∞)上单调递增,y=x-1在(-∞,0)上单调递增,且x-1<0,x2≥0;
∴函数f(x)在R上是增函数;
∴由f(m2)>f(m+2)得m2>m+2,解得m<-1,或m>2;
若p∨q为真,p∧q为假,则p,q一真一假;
∴p真q假时,$\left\{\begin{array}{l}{m<2}\\{-1≤m≤2}\end{array}\right.$,
∴-1≤m<2;
p假q真时,$\left\{\begin{array}{l}{m≥2}\\{m<-1,或m>2}\end{array}\right.$,
∴m>2;
∴m的取值范围为[-1,2)∪(2,+∞).
点评 考查定积分的计算,二次函数的单调性,一次函数的单调性,以及分段函数单调性的判断方法,p∨q.p∧q真假和p,q真假的关系,属于中档题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
16.复数z=$\frac{-2i}{1+i}$的虚部为( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
17.深圳市某学校为了了解学生使用手机与学习成绩之间的关系,抽查了有手机同学40名,其中成绩为优秀的人数24名,抽查没有手机同学20人,其中成绩为优秀的人数15名,
(1)根据以上数据完成下面的2×2列联表(单位:人)
(2)根据题(1)中表格的数据计算,你有多大的把握,认为学生手机与成绩之间有关系?
(1)根据以上数据完成下面的2×2列联表(单位:人)
| 拥有手机 | 没有手机 | 合计 | |
| 成绩优秀 | |||
| 成绩不优势 | |||
| 合计 |
10.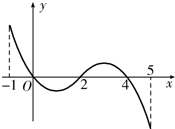 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,
f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数
y=f(x)-a的零点的个数为( )
 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
y=f(x)-a的零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.总体编号为001,002,003,…,299,300的300个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第3、4、5列数字开始由左到右依次选取三个数字,则选出来的第5个个体的编号为( )


| A. | 080 | B. | 263 | C. | 140 | D. | 280 |
15.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,若∠B=2∠A,且a:b=1:$\sqrt{3}$,则cos2B的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |