题目内容
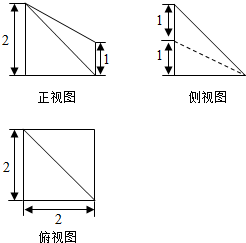
5.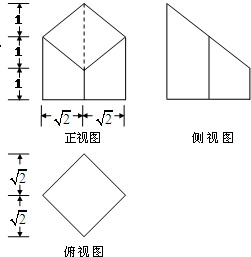 某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).
某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).
分析 三视图复原的几何体是长方体的三分之二,依据三视图的数据,得出长方体长、宽、高,即可求出几何体的表面积.
解答 解:三视图复原的几何体是长方体,长方体长、宽、高分别是:2,2,3,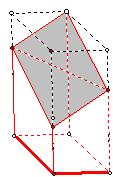
几何体的底面为正方形,面积为:2×2=4,
几何体的侧面为四个直角梯形,面积为:2×$\frac{1}{2}$(1+2)×2+2×$\frac{1}{2}$(2+3)×2=16,
几何体的截面是一个边长为$\sqrt{5}$的菱形,且两条对角线长度分别为:2$\sqrt{2}$和2$\sqrt{3}$,面积为:$\frac{1}{2}$×$2\sqrt{2}×2\sqrt{3}$=2$\sqrt{6}$,
故几何体的全面积为:20+2$\sqrt{6}$,
故答案为:20+2$\sqrt{6}$.
点评 本题考查的知识点是简单空间图象的三视图,其中根据已知中的视图分析出几何体的形状及棱长是解答的关键.

练习册系列答案
相关题目
17.如果复数$\frac{2-bi}{3+i}$(b∈R)的实部与虚部互为相反数,则b=( )
| A. | 0 | B. | 1 | C. | -l | D. | ±1 |
14.以双曲线$\frac{{x}^{2}}{10}$-$\frac{{y}^{2}}{15}$=1的右焦点为圆心,且与其渐近线相切的圆的方程是( )
| A. | x2+y2-10x+10=0 | B. | x2+y2-10x+15=0 | C. | x2+y2+10x+15=0 | D. | x2+y2+10x+10=0 |