题目内容
10.数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n},(0≤an<\frac{1}{2})}\\{2{a}_{n}-1,(\frac{1}{2}≤{a}_{n}<1)}\end{array}\right.$,若a1=$\frac{6}{7}$,则a2010=$\frac{3}{7}$.分析 通过计算前几项的值,确定周期,进而可得结论.
解答 解:根据题意可得:a2=2×$\frac{6}{7}$-1=$\frac{5}{7}$,
a3=2×$\frac{5}{7}$-1=$\frac{3}{7}$,
a4=2×$\frac{3}{7}$=$\frac{6}{7}$,
a5=2×$\frac{6}{7}$-1=$\frac{5}{7}$,
…
∴数列{an}是以3为周期的数列,
∵2010=3×670,
∴a2010=a3=$\frac{3}{7}$,
故答案为:$\frac{3}{7}$.
点评 本题考查求数列的通项,找出周期是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
20.已知双曲线C 的一个焦点与抛物线y2=8$\sqrt{3}$x的焦点相同,且双曲线C过点P(-2,0),则双曲线C的渐近线方程是( )
| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{{\sqrt{2}}}{2}$ | C. | xy=±2$\sqrt{2}$x | D. | y=±$\sqrt{11}$x |
20.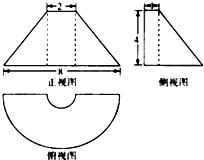 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )| A. | 12π | B. | 16π | C. | 20π | D. | 24π |
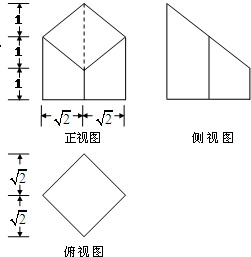 某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).
某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).