题目内容
16.已知函数f(x)=$\overrightarrow{m}$.$\overrightarrow{n}$,且$\overrightarrow{m}$=(sinωx+cosωx,$\sqrt{3}$cosωx),$\overrightarrow{n}$=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)相邻两对称轴的距离大于等于$\frac{π}{2}$.(1)求ω的取值范围;
(2)在锐角三角形△ABC中,a,b,c分别是角A,B,C的对边,当ω最大时,f(A)=1,且a=$\sqrt{3}$,求c+b的取值范围.
分析 (1)根据二倍角公式和和差角公式(辅助角公式),化简函数解析式为正弦型函数的形式,进而结合相邻两对称轴的距离大于等于$\frac{π}{2}$.可得f(x)的最小正周期,求出ω的取值范围;
(2)由正弦定理可得b=2sinB,c=2sinC,再由B,C的关系,求得B的范围,结合两角和的正弦公式,以及正弦函数的图象和性质,即可得到所求范围.
解答 解:(1)∵函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=cos2ωx-sin2ωx+2$\sqrt{3}$sinωxcosωx
=cos2ωx+$\sqrt{3}$sin2ωx=2($\frac{1}{2}$cos2ωx+$\frac{\sqrt{3}}{2}$sin2ωx)=2sin(2ωx+$\frac{π}{6}$),
由题意得$\frac{T}{2}$≥$\frac{π}{2}$,即T≥π,
又∵ω>0,
∴$\frac{2π}{2ω}$≥π,
∴0<ω≤1;
(2)当ω最大时,即有ω=1,f(x)=2sin(2x+$\frac{π}{6}$),
∵f(A)=2sin(2A+$\frac{π}{6}$)=1,∴sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,
∵0<A<$\frac{π}{2}$,∴2A+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{7π}{6}$),2A+$\frac{π}{6}$=$\frac{5π}{6}$,
∴A=$\frac{π}{3}$,
由正弦定理可得$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{\sqrt{3}}{sin\frac{π}{3}}$=2,
则b=2sinB,c=2sinC,
b+c=2sinB+2sinC=2sinB+2sin($\frac{2π}{3}$-B)
=$\sqrt{3}$cosB+3sinB=2$\sqrt{3}$sin(B+$\frac{π}{6}$),
在锐角三角形ABC中,0$<B<\frac{π}{2}$,0<$C<\frac{π}{2}$,
即有0<$\frac{2π}{3}$-B<$\frac{π}{2}$,可得$\frac{π}{6}$<B<$\frac{π}{2}$,
可得$\frac{π}{3}$<B+$\frac{π}{6}$<$\frac{2π}{3}$,
$\frac{\sqrt{3}}{2}$<sin(B+$\frac{π}{6}$)≤1,即有3<2$\sqrt{3}$sin(B+$\frac{π}{6}$)≤2$\sqrt{3}$,
则b+c的取值范围是(3,2$\sqrt{3}$].
点评 本题考查的知识点是三角函数中的恒等变换应用,平面向量数量积的运算,正弦定理和余弦定理,是三角函数与向量的综合应用,难度中档.

 备战中考寒假系列答案
备战中考寒假系列答案
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
| A. | $\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | $\frac{1}{2}+\frac{5}{2}i$ | B. | $\frac{1}{2}-\frac{5}{2}i$ | C. | $-\frac{1}{2}+\frac{5}{2}i$ | D. | $-\frac{1}{2}-\frac{5}{2}i$ |
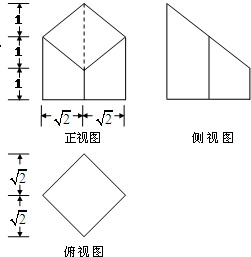 某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).
某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).