题目内容
15.在直角坐标系xOy 中,曲线C1的参数方程为$\left\{\begin{array}{l}x=1+cos2α\\ y=\frac{1}{2}cosα\end{array}$(α为参数),在极坐标系中,曲线C2的极坐标方程为ρsin(θ-$\frac{π}{4}$)=$\sqrt{2}$(1)求曲线C2的普通方程
(2)设c1与c2相交于A,B两点,求|AB|的长.
分析 (1)用极坐标公式,即可把曲线C2的极坐标方程化为普通方程;
(2)把曲线C1的参数方程化为普通方程,利用直线与抛物线C2的方程,
求出直线与抛物线没有交点.
解答 解:(1)将曲线C2的极坐标方程$ρsin(θ-\frac{π}{4})=\sqrt{2}$展开,
得:ρsinθ-ρcosθ=2,
化为普通方程是:y-x=2;①
(2)将C1的参数方程$\left\{\begin{array}{l}{x=1+cos2α}\\{y=\frac{1}{2}cosα}\end{array}\right.$,
∵x=1+2cos2α-1=2cos2α,
y2=$\frac{1}{4}$cos2α,
∴8y2=2cos2α,
化为普通方程是:
y2=$\frac{1}{8}$x②;
所以直线经过该抛物线的焦点F($\frac{1}{32}$,0);
由①、②联立,消去x得:
y2-$\frac{1}{8}$y+$\frac{1}{4}$=0;
∴△=${(\frac{1}{8})}^{2}$-4×$\frac{1}{4}$=-$\frac{63}{64}$<0,
∴c1与c2不会交于两点.
点评 本题考查了直线与抛物线的应用问题,也考查了参数方程与极坐标的应用问题,是综合题.

练习册系列答案
相关题目
10.已知抛物线x2=-4$\sqrt{5}$y的焦点与双曲线$\frac{x^2}{a}+\frac{y^2}{4}$=1(a∈R)的一焦点重合,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
20.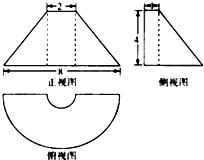 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )| A. | 12π | B. | 16π | C. | 20π | D. | 24π |
7.直线l:8x-6y-3=0被圆O:x2+y2-2x+a=0所截得弦的长度为$\sqrt{3}$,则实数a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 1-$\frac{{\sqrt{13}}}{2}$ |
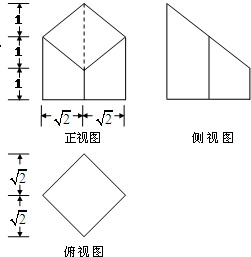 某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).
某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).
 根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015
根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015