题目内容
17.如果复数$\frac{2-bi}{3+i}$(b∈R)的实部与虚部互为相反数,则b=( )| A. | 0 | B. | 1 | C. | -l | D. | ±1 |
分析 直接利用复数的乘除运算法则,化简,然后利用已知条件求解即可.
解答 解:复数$\frac{2-bi}{3+i}$=$\frac{(2-bi)(3-i)}{(3+i)(3-i)}$=$\frac{6-b-(2+3b)i}{10}$.
复数$\frac{2-bi}{3+i}$(b∈R)的实部与虚部互为相反数,
可得6-b=2+3b,解得b=1.
故选:B.
点评 本题考查复数代数形式的混合运算,复数的基本概念,考查计算能力.

练习册系列答案
相关题目
7.若执行如图所示的程序框图,则输出的i的值为( )
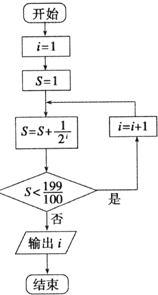

| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
12.如图所示的程序框图运行结束后,输出的集合中包含的元素个数为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7.直线l:8x-6y-3=0被圆O:x2+y2-2x+a=0所截得弦的长度为$\sqrt{3}$,则实数a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 1-$\frac{{\sqrt{13}}}{2}$ |
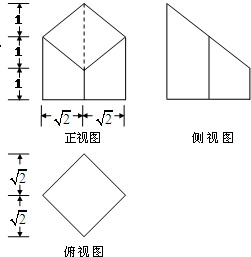 某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).
某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).