题目内容
20.已知某几何体的三视图如图所示,则该几何体的体积为$\frac{10}{3}$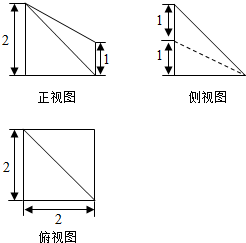
分析 几何体是直三棱柱消去一个三棱锥,结合直观图分别求出直三棱柱的体积和消去的三棱锥的体积,相减可得几何体的体积.
解答 解:由三视图知:几何体是直三棱柱消去一个三棱锥,如图:
直三棱柱的体积为$\frac{1}{2}$×2×2×2=4.
消去的三棱锥的体积为$\frac{1}{3}$×$\frac{1}{2}$×2×1×2=$\frac{2}{3}$,
∴几何体的体积V=4-$\frac{2}{3}$=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题考查了由三视图求几何体的表面积,根据三视图判断几何体的形状及相关几何量的数据是解答此类问题的关键.

练习册系列答案
相关题目
11.复数$\frac{3+2i}{1-i}$=( )
| A. | $\frac{1}{2}+\frac{5}{2}i$ | B. | $\frac{1}{2}-\frac{5}{2}i$ | C. | $-\frac{1}{2}+\frac{5}{2}i$ | D. | $-\frac{1}{2}-\frac{5}{2}i$ |
15.点P在直径为5的球面上,过P作两两互相垂直的三条弦(两端点均在球面上的线段),若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
| A. | 2$\sqrt{14}$ | B. | 2$\sqrt{70}$ | C. | $\sqrt{70}$ | D. | $\sqrt{14}$ |
12.如图所示的程序框图运行结束后,输出的集合中包含的元素个数为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
10.已知抛物线x2=-4$\sqrt{5}$y的焦点与双曲线$\frac{x^2}{a}+\frac{y^2}{4}$=1(a∈R)的一焦点重合,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
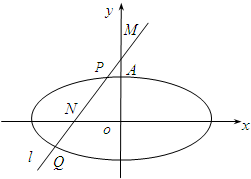 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.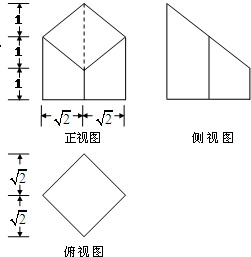 某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).
某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的全面积为20+2$\sqrt{6}$(平方单位).