题目内容
【题目】已知椭圆
： 
的离心率为
， 
为该椭圆的右焦点，过点
任作一直线
交椭圆于
两点，且
的最大值为4.
（1）求椭圆
的方程；
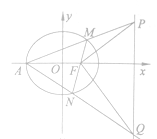
（2）设椭圆
的左顶点为
，若直线
分别交直线
于
两点，求证： 
.
【答案】（1）
；（2）证明见解析.
【解析】试题分析：（1）根据题意列出关于
、
、
的方程组，结合性质
， ，求出
、
、
，即可得结果；（2）直线
，直线与曲线联立得
，根据韦达定理，化简可得
，从而可得结果.
试题解析：（1）依题意知： 
， 
，
即
；
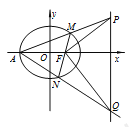
所求椭圆
的方程： 
．
（2）由（1）知
， 
；
（ⅰ）当直线
斜率不存在时， 
；
直线
；
所以
,同理
；即
；
即
；所以
．
（ⅱ）当直线
斜率存在时，设直线
，
，
由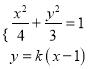
得： 
即
， 
，
由
三点共线得： 
，同理
即
, 
,
∴
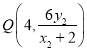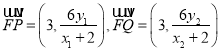
即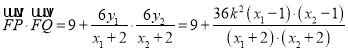
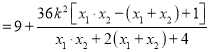
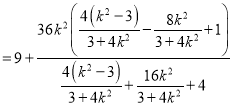
所以
．
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式，属于难题.用待定系数法求椭圆方程的一般步骤；①作判断：根据条件判断椭圆的焦点在
轴上，还是在
轴上，还是两个坐标轴都有可能；②设方程：根据上述判断设方程
或
；③找关系：根据已知条件，建立关于
、
、
的方程组；④得方程：解方程组，将解代入所设方程，即为所求.
练习册系列答案
相关题目
