题目内容
【题目】已知函数f(x)对任意的x,y∈R,总有f(x)+f(y)=f(x+y),且x<0时,f(x)>0.
(1)求证:函f(x)是奇函数;
(2)求证:函数f(x)是R上的减函数;
(3)若定义在(﹣2,2)上的函数f(x)满足f(﹣m)+f(1﹣m)<0,求实数m的取值范围.
【答案】
(1)证明:∵f(x+y)=f(x)+f(y)
∴令x=y=0 有f (0 )=0
令y=﹣x 有:0=f(0)=f(x+(﹣x))=f(x)+f(﹣x)
∴函数f(x)是奇函数
(2)证明:设x2>x1则x1﹣x2<0
∵当x<0时,f(x)>0
∴f(x1﹣x2)>0
∴f(x1)=f[(x1﹣x2)+x2]=f(x1﹣x2)+f(x2)>f(x2)
∴函数f(x)是R上的减函数
(3)解:∵f(﹣m)+f(1﹣m)<0,∴f(﹣m)<f(m﹣1),
且f(﹣m)+f(1﹣m)=f(1﹣2m)
∴ 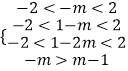 ,解得:﹣
,解得:﹣ ![]() <m<
<m< ![]()
【解析】(1)由f(x+y)=f(x)+f(y)可令x=y=0 有f (0 )=0,令y=﹣x 代入即证;(2)设x2>x1则x1﹣x2<0,由已知当x<0时,f(x)>0可得f(x1﹣x2)>0,则f(x1)=f[(x1﹣x2)+x2]=f(x1﹣x2)+f(x2)>f(x2)可证;(3)移项,利用奇偶性进行化简,然后利用单调性建立不等式,注意定义域,从而可求出m的取值范围.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较,以及对函数的奇偶性的理解,了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称.

【题目】 某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (
(![]() 为大于
为大于![]() 的常数),现随机抽取
的常数),现随机抽取![]() 件合格产品,测得数据如下:
件合格产品,测得数据如下:
尺寸 |
|
|
|
|
|
|
质量 |
|
|
|
|
|
|
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的
内时为优等品,现从抽取的![]() 件合格产品中再任选
件合格产品中再任选![]() 件,记
件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望.
的分布列和期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
【题目】为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:

(Ⅰ)是否有![]() 的把握认为入院者中患肺心病与性别有关?请说明理由;
的把握认为入院者中患肺心病与性别有关?请说明理由;
(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.