题目内容
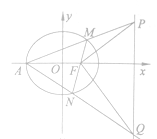
【题目】如图,三棱柱![]() 的所有棱长均为2,平面
的所有棱长均为2,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)证明: ![]() ;
;
(2)若![]() 是棱
是棱![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2) 所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】试题分析:(1)证线线垂直,由平面![]() 平面
平面![]() 得
得![]() 平面
平面![]() ,再由底面图形得线线垂直.(2)建系求面的法向量,得法向量的夹角.
,再由底面图形得线线垂直.(2)建系求面的法向量,得法向量的夹角.
解:
(1)证明:取![]() 中点
中点![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
, ![]() ,依题意得
,依题意得![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为四边形![]() 为菱形,所以
为菱形,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解:由(1)结合已知得: ![]() ,
, ![]() ,
, ![]() ,
,
以![]() 为原点,如图所示建立空间直角坐标系
为原点,如图所示建立空间直角坐标系![]() ,因为侧面
,因为侧面![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 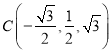 ,
,
所以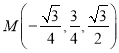 ,
, ![]() ,
, 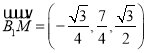 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则由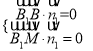 得
得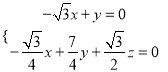 ,令
,令![]() ,可取
,可取![]() ,
,
而平面![]() 的一个法向量
的一个法向量![]() ,由图可知二面角
,由图可知二面角![]() 为锐角,
为锐角,
因为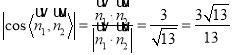 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案【题目】 某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (
(![]() 为大于
为大于![]() 的常数),现随机抽取
的常数),现随机抽取![]() 件合格产品,测得数据如下:
件合格产品,测得数据如下:
尺寸 |
|
|
|
|
|
|
质量 |
|
|
|
|
|
|
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的
内时为优等品,现从抽取的![]() 件合格产品中再任选
件合格产品中再任选![]() 件,记
件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望.
的分布列和期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
【题目】为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:

(Ⅰ)是否有![]() 的把握认为入院者中患肺心病与性别有关?请说明理由;
的把握认为入院者中患肺心病与性别有关?请说明理由;
(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.