题目内容
【题目】(本小题满分12分)已知数列{an}是等差数列,且a1,a2(a1<a2)分别为方程x2﹣6x+5=0的二根.
(1)求数列{an}的前n项和Sn;
(2)在(1)中,设bn=![]() ,求证:当c=﹣
,求证:当c=﹣![]() 时,数列{bn}是等差数列.
时,数列{bn}是等差数列.
【答案】(1)![]() ,(2)略
,(2)略
【解析】试题分析:解一元二次方程得出![]() 和
和![]() ,有公差
,有公差![]() ,写出等差数列的前
,写出等差数列的前![]() 项和,写出
项和,写出![]() ,代入
,代入![]() ,证明数列{bn}是等差数列,只需证明
,证明数列{bn}是等差数列,只需证明![]() 为一个常数.
为一个常数.
试题解析:
(1)解方程x2﹣6x+5=0得其二根分别为1和5,
∵a1,a2(a1<a2)分别为方程x2﹣6x+5=0的二根
∴以a1=1,a2=5,
∴{an}等差数列的公差为4,
∴![]() =2n2﹣n;
=2n2﹣n;
(2)证明:当![]() 时,
时,![]() =
=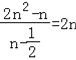 ,
,
∴bn+1﹣bn=2(n+1)﹣2n=2,
∴{bn}是以2为首项,公差为2的等差数列.

练习册系列答案
相关题目