题目内容
3.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
分析 利用向量数量积运算性质即可得出.
解答 解:∵向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,
则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
故选:A.
点评 本题考查了向量数量积运算性质,属于基础题.

练习册系列答案
相关题目
14.已知函数f(x)=x2•sinx,各项均不相等的数列{xn}满足|xi|≤$\frac{π}{2}$(i=1,2,3,…,n).令F(n)=(x1+x2+…+xn)•[f(x1)+f(x2)+…f(xn)](n∈N*).给出下列三个命题:
(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
11.函数f(x)=sinx+sin($\frac{2π}{3}$-x)的图象的一条对称轴为( )
| A. | x=$\frac{π}{2}$ | B. | x=π | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |
8.等差数列{an}的前n项和为Sn,且a1+a2=10,S4=36,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量是( )
| A. | $(-\frac{1}{2},-2)$ | B. | (-1,-1) | C. | $(-\frac{1}{2},-1)$ | D. | (2,$\frac{1}{2}$) |
10. 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 |
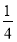 圆弧)( )
圆弧)( )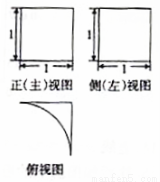
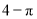 B.
B.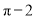
 D.
D.