题目内容
8.等差数列{an}的前n项和为Sn,且a1+a2=10,S4=36,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量是( )| A. | $(-\frac{1}{2},-2)$ | B. | (-1,-1) | C. | $(-\frac{1}{2},-1)$ | D. | (2,$\frac{1}{2}$) |
分析 由题意求出等差数列的通项公式,得到P,Q的坐标,写出向量 $\overrightarrow{PQ}$的坐标,找到与向量 $\overrightarrow{PQ}$共线的坐标即可.
解答 解:等差数列{an}中,设首项为a1,公差为d,
由S2=10,S4=36,得$\left\{\begin{array}{l}2{a}_{1}+d=10\\ 4{a}_{1}+6d=36\end{array}\right.$,解得a1=3,d=4.
∴an=a1+(n-1)d=3+4(n-1)=4n-1.
则P(n,4n-1),Q(n+2,4n+7).
∴过点P和Q的直线的一个方向向量的坐标可以是(2,8)=-4(-$\frac{1}{2}$,-2).即为(-$\frac{1}{2}$,-2).
故选:A.
点评 本题考查了直线的斜率,考查了等差数列的通项公式,训练了向量的坐标表示,是中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
3.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
12.已知不共线向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
15.某高三同学在七次月考考试中,数学成绩如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
| A. | 92,2 | B. | 92,2.8 | C. | 93,2 | D. | 93,2.8 |
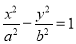 (
(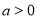 ,
,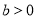 )经过点
)经过点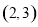 ,且离心率为
,且离心率为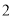 ,则它的焦距为( )
,则它的焦距为( )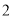 B.
B.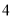
 D.
D.