题目内容
11.函数f(x)=sinx+sin($\frac{2π}{3}$-x)的图象的一条对称轴为( )| A. | x=$\frac{π}{2}$ | B. | x=π | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |
分析 先化简函数,再利用正弦函数的性质,即可得出结论.
解答 解:f(x)=sinx+sin($\frac{2π}{3}$-x)=sinx+$\frac{\sqrt{3}}{2}$cosx+$\frac{1}{2}$sinx=$\sqrt{3}$sin(x+$\frac{π}{6}$),
∴x=$\frac{π}{3}$是函数f(x)=sinx+sin($\frac{2π}{3}$-x)的图象的一条对称轴,
故选:D.
点评 本题考查三角函数的化简,考查正弦函数的性质,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
18.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),M、N为双曲线上关于原点对称的两点,P为双曲线上的点,且直线PM、PN斜率分别为k1、k2,若k1•k2=$\frac{5}{4}$,则双曲线离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
 .
. 对其定义域内任意
对其定义域内任意 成立,求
成立,求 值;
值; 时,求
时,求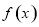 在区间
在区间 上的最值.
上的最值.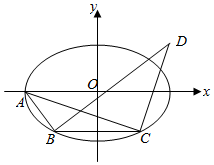 如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.