题目内容
18.若将函数f(x)=|sin(ωx-$\frac{π}{6}$)|(ω>0)的图象向左平移$\frac{π}{9}$个单位后,所得图象对应的函数为偶函数,则实数ω的最小值是$\frac{3}{2}$.分析 由函数y=Asin(ωx+φ)的图象变换可得f(x)=|sin[ωx+($\frac{πω}{9}$-$\frac{π}{6}$)]|,由$\frac{πω}{9}$-$\frac{π}{6}$=$\frac{kπ}{2}$,解得ω=$\frac{9k}{2}$+$\frac{3}{2}$时,从而可求实数ω的最小值.
解答 解:f(x)=|sin[ω(x+$\frac{π}{9}$)-$\frac{π}{6}$]|=|sin[ωx+($\frac{πω}{9}$-$\frac{π}{6}$)]|
∵当$\frac{πω}{9}$-$\frac{π}{6}$=$\frac{kπ}{2}$时,即ω=$\frac{9k}{2}$+$\frac{3}{2}$时,
f(x)=|sin(ωx-$\frac{kπ}{2}$)|=|-cos(ωx)|=|cos(ωx)|,f(x)为偶函数.
∴当k=0时,ω有最小值=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换,三角函数的图象与性质,属于基本知识的考查.

练习册系列答案
相关题目
13.已知数列{an}满足a1=3,且an+1=4an+3(n∈N*),则数列{an}的通项公式为( )
| A. | 22n-1+1 | B. | 22n-1-1 | C. | 22n+1 | D. | 22n-1 |
 个小组的频率之比为
个小组的频率之比为 ,其中第
,其中第 小组的频数为
小组的频数为 ,则这批学生中的总人数为___________.
,则这批学生中的总人数为___________.
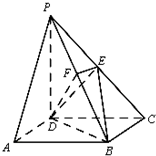 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.