题目内容
14.已知函数f(x)=x2•sinx,各项均不相等的数列{xn}满足|xi|≤$\frac{π}{2}$(i=1,2,3,…,n).令F(n)=(x1+x2+…+xn)•[f(x1)+f(x2)+…f(xn)](n∈N*).给出下列三个命题:(1)存在不少于3项的数列{xn},使得F(n)=0;
(2)若数列{xn}的通项公式为${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,则F(2k)>0对k∈N*恒成立;
(3)若数列{xn}是等差数列,则F(n)≥0对n∈N*恒成立.
其中真命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
分析 由题意,f(x)=x2sinx是奇函数,只需考查0<x≤1时的性质,此时y=x2,y=sinx都是增函数,得f(x)=x2sinx在[0,1]上是增函数;即x1+x2≠0时,(x1+x2)(f(x1)+f(x2))>0;
对于(1),取$-\frac{π}{2}$≤x1=-x3$≤\frac{π}{2}$,x2=0,即可判断;
对于(2),运用等比数列的求和公式和性质,即可判断;
对于(3),运用等差数列的求和公式和性质,结合函数f(x)的单调性,即可判断.
解答 解:由题意得f(x)=x2sinx是奇函数,
当0<x≤$\frac{π}{2}$时,y=x2,y=sinx都是增函数,
∴f(x)=x2sinx在[0,$\frac{π}{2}$]上递增,
∴f(x)=x2sinx在[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数;
若x1+x2<0,则x1<-x2,∴f(x1)<f(-x2),
即f(x1)<-f(x2),∴f(x1)+f(x2)<0;
同理若x1+x2>0,可得f(x1)+f(x2)>0;
∴x1+x2≠0时,(x1+x2)(f(x1)+f(x2))>0.
对于(1),取$-\frac{π}{2}$≤x1=-x3$≤\frac{π}{2}$,x2=0,则F(3)=(x1+x2+x3)•
[f(x1)+f(x2)+f(x3)]=0,因此(1)正确;
对于(2),∵${x_n}={({-\frac{1}{2}})^n}({n∈{N^*}})$,∴x1+x2+…+xn=$\frac{-\frac{1}{2}[1-(-\frac{1}{2})^{n}]}{1-(-\frac{1}{2})}$<0,
又f(2k-1)+f(2k)=$(-\frac{1}{2})^{2(2k-1)}$$sin(-\frac{1}{2})^{2k-1}$+$(-\frac{1}{2})^{2•2k}$$sin(-\frac{1}{2})^{2k}$=$(\frac{1}{4})^{2k}$$[-4sin(\frac{1}{2})^{2k-1}+sin(\frac{1}{2})^{2k}]$<0,
∴F(2k)>0对k∈N*恒成立,故(2)正确;
对于(3),如x1+x2+…+xn=0,F(n)=0时,若数列{xn}是等差数列,
则x1+x2+…+xn>0,则x1+xn>0,f(x1)>f(xn),可得x2+xn-1>0,…,f(x2)>f(xn-1),…
相加即可得到F(n)>0,同理x1+x2+…+xn<0,即有f(x1)+f(x2)+…f(xn)<0,即F(n)>0,
则(3)正确.
故选D.
点评 本题通过命题真假的判定,考查了新定义的函数的性质以及应用问题,函数的单调性与奇偶性问题,等差与等比数列的性质与应用问题,是综合题.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案 ,
,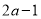 ,
,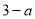 .则这个数列的通项公式为_______.
.则这个数列的通项公式为_______. :
: (
(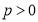 )与椭圆
)与椭圆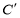 :
: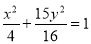 相交所得的弦长为
相交所得的弦长为
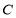 的标准方程;
的标准方程;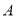 ,
,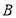 是
是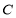 上异于原点
上异于原点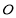 的两个不同点,直线
的两个不同点,直线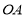 和
和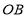 的倾斜角分别为
的倾斜角分别为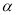 和
和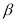 ,当
,当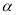 ,
,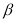 变化且
变化且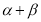 为定值
为定值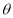 (
(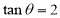 )时,证明:直线
)时,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.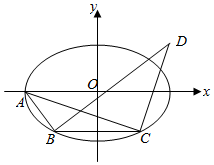 如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.