题目内容
10. 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 |
分析 由题意,B1C为B1D在平面BCC1B1中的射影,存在点E,使得B1D⊥EC1,则B1C⊥EC1,即可得出结论.
解答 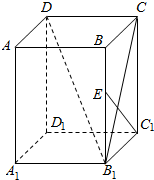 解:由题意,B1C为B1D在平面BCC1B1中的射影,存在点E,使得B1D⊥EC1,则B1C⊥EC1,
解:由题意,B1C为B1D在平面BCC1B1中的射影,存在点E,使得B1D⊥EC1,则B1C⊥EC1,
当a>b时,过C1点垂直B1C的直线交于BC上,
所以当且仅当a≤b时,存在点E,使得B1D⊥EC1,
故选:D.
点评 本题考查线面垂直,考查学生分析解决问题的能力,确定B1C为B1D在平面BCC1B1中的射影是关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
3.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
18.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),M、N为双曲线上关于原点对称的两点,P为双曲线上的点,且直线PM、PN斜率分别为k1、k2,若k1•k2=$\frac{5}{4}$,则双曲线离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
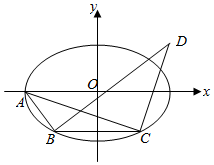 如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.
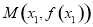 和点
和点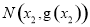 分别是函数
分别是函数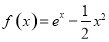 和
和 图象上的点,且
图象上的点,且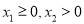 .若直线
.若直线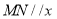 轴,则
轴,则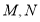 两点间的距离的最小值为( )
两点间的距离的最小值为( )