题目内容
10.已知函数f(x)=$\frac{1+lnx}{x}$.(Ⅰ)求函数f(x)在x=1处的切线方程.
(Ⅱ)若a为实数,函数f(x)在区间(a,a+1)上的有极值,求a的取值范围;
(Ⅲ)试问是否存在k,b∈N,使得ex>kx+b>f(x)恒成立?若存在,请写出k,b的值,并证明你的结论;若不存在,请说明理由.
分析 (Ⅰ)求导数,确定切线的斜率,即可求函数f(x)在x=1处的切线方程.
(Ⅱ)求导数,确定函数的单调性,可得函数f(x)在x=1处取得极大值,利用函数f(x)在区间(a,a+1)上的有极值,即可求a的取值范围;
(Ⅲ)证明k=2,b=0时命题成立,即证ex>kx+b>f(x)恒成立,构造函数,确定函数的单调性可得结论;
解答 解:(Ⅰ)因为$f'(x)=-\frac{lnx}{x^2}$,f'(1)=0…1分
所以函数f(x)在x=1处的切线方程为y=1…3分
(Ⅱ)因为$f(x)=\frac{1+lnx}{x}$,x>0,由$f'(x)=-\frac{lnx}{x^2}$,令f'(x)=0,得x=1
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0…4分
所以f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减.
所以函数f(x)在x=1处取得极大值.…5分
因为函数f(x)在区间(a,a+1)上有极值,
所以a<1<a+1,解得0<a<1.…7分
(III)因为y=ex过点(0,1),结合函数y=ex的图象可知,当b≥1时,直线y=kx+b与函数y=ex的图象恒有公共点,不合题意,所以b<1,又b∈N,故b=0.
在不等式ex>kx+b>f(x)中,令x=1,得e>k>1,又k∈N,所以k=2.
以下证明k=2,b=0时命题成立,即证ex>kx+b>f(x)恒成立…8分
方法一:因为${e^x}>2x>f(x)?\frac{e^x}{x}>2>\frac{1+lnx}{x^2}$.(*)
( i)设$g(x)=\frac{e^x}{x}$,则$g'(x)=\frac{{x{e^x}-{e^x}}}{x^2}$,令g'(x)=0,得x=1.
则g(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增.
所以g(x)≥g(1)=e>2,即不等式$\frac{e^x}{x}>2$成立.…10分
( ii)设$h(x)=\frac{1+lnx}{x^2}$,则$h'(x)=\frac{x-2x(1+lnx)}{x^4}=-\frac{1+2lnx}{x^3}(x>0)$,
令h'(x)=0,得$x=\frac{1}{{\sqrt{e}}}$,
则h(x)在区间$(0,\frac{1}{{\sqrt{e}}})$上单调递增,在区间$(\frac{1}{{\sqrt{e}}},+∞)$上单调递减.
所以$h(x)≤h(\frac{1}{{\sqrt{e}}})=\frac{e}{2}<2$,即不等式$\frac{1+lnx}{x^2}<2$成立.…13分
综上可知(*)式成立,即存在k=2,b=0满足题意.…14分
方法二:ex>2x>f(x)等价于ex>2x,且2x2>1+lnx.(*)
( i)设g(x)=ex-2x,g'(x)=ex-2.令g'(x)=0,得x=ln2.
则g(x)在区间(0,ln2)上单调递减,在区间(ln2,+∞)上单调递增.
所以g(x)≥g(ln2)=2-ln2=2(1-ln2)>0,即ex>2x恒成立.…10分
( ii)设h(x)=2x2-lnx-1,则$h'(x)=4x-\frac{1}{x}(x>0)$,令h'(x)=0,得$x=\frac{1}{2}$,
则h(x)在区间$(0,\frac{1}{2})$上单调递减,在区间$(\frac{1}{2},+∞)$上单调递增.
所以$h(x)≥h(\frac{1}{2})=\frac{1}{2}-ln\frac{1}{2}-1=ln2-\frac{1}{2}>ln\sqrt{e}-\frac{1}{2}=0$,
即2x2>1+lnx恒成立.…13分
综上可知(*)式成立,即存在k=2,b=0满足题意.…14分.
点评 本题考查导数知识的综合运用,考查函数的单调性,考查导数的几何意义,考查学生分析解决问题的能力,有难度.

 名校课堂系列答案
名校课堂系列答案| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
| A. | 92,2 | B. | 92,2.8 | C. | 93,2 | D. | 93,2.8 |

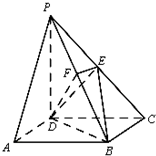 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.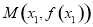 和点
和点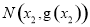 分别是函数
分别是函数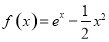 和
和 图象上的点,且
图象上的点,且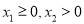 .若直线
.若直线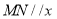 轴,则
轴,则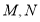 两点间的距离的最小值为( )
两点间的距离的最小值为( )