题目内容
14.设F1,F2分别为椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,点A为椭圆E的左顶点,点B为椭圆E的上顶点,且|AB|=2.(Ⅰ)若椭圆E的离心率为$\frac{{\sqrt{6}}}{3}$,求椭圆E的方程;
(Ⅱ)设P为椭圆E上一点,且在第一象限内,直线F2P与y轴相交于点Q.若以PQ为直径的圆经过点F1,证明:点P在直线x+y-2=0上.
分析 (Ⅰ)通过题意可得A(-a,0)、B(0,b),利用|AB|=2、$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{{\sqrt{6}}}{3}$,计算即可;
(Ⅱ)设P(x0,y0),由题意知x0≠c,利用${k}_{{F}_{1}P}$•${k}_{{F}_{1}Q}$=-1、$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{4-{a}^{2}}$=1,x0、y0>0,计算即可.
解答 (Ⅰ)解:∵点A为椭圆E的左顶点,点B为椭圆E的上顶点,
∴A(-a,0),B(0,b),
又∵|AB|=2,∴a2+b2=4,
∵e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{{\sqrt{6}}}{3}$,
∴a=$\sqrt{3}$,b=1,
∴椭圆E的方程为:$\frac{{x}^{2}}{3}$+y2=1;
(Ⅱ)证明:由题意知a2+b2=4,从而椭圆E的方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{4-{a}^{2}}$=1,
则F1(-c,0),F2(c,0),c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{2{a}^{2}-4}$,
设P(x0,y0),由题意知x0≠c,
则直线F1P的斜率${k}_{{F}_{1}P}$=$\frac{{y}_{0}}{c+{x}_{0}}$,直线F2P的斜率${k}_{{F}_{2}P}$=$\frac{{y}_{0}}{{x}_{0}-c}$,
∴直线F2P的方程为:y=$\frac{{y}_{0}}{{x}_{0}-c}$(x-c),
当x=0时,y=-$\frac{{y}_{0}}{{x}_{0}-c}$c,即点Q(0,-$\frac{{y}_{0}}{{x}_{0}-c}$c),
∴直线F1Q的斜率${k}_{{F}_{1}Q}$=$\frac{{y}_{0}}{c-{x}_{0}}$,
∵以PQ为直径的圆经过点F1,
∴PF1⊥F1Q,∴${k}_{{F}_{1}P}$•${k}_{{F}_{1}Q}$=$\frac{{y}_{0}}{c+{x}_{0}}$•$\frac{{y}_{0}}{c-{x}_{0}}$=-1,
化简得:${{y}_{0}}^{2}$=${{x}_{0}}^{2}$-(2a2-4),①
又∵P为椭圆E上一点,且在第一象限内,
∴$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{4-{a}^{2}}$=1,x0、y0>0,②
由①②,解得x0=$\frac{{a}^{2}}{2}$,y0=2-$\frac{1}{2}$a2,
∴x0+y0=2,即点P在直线x+y-2=0上.
点评 本题考查椭圆的定义及其标准方程、直线与圆的位置关系、斜率等基础知识,考查运算求解能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案 :
: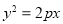 (
(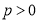 )与椭圆
)与椭圆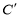 :
: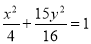 相交所得的弦长为
相交所得的弦长为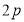
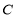 的标准方程;
的标准方程;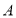 ,
,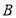 是
是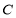 上异于原点
上异于原点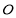 的两个不同点,直线
的两个不同点,直线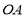 和
和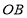 的倾斜角分别为
的倾斜角分别为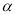 和
和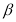 ,当
,当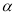 ,
,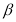 变化且
变化且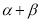 为定值
为定值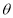 (
(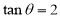 )时,证明:直线
)时,证明:直线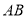 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.