题目内容
(1)求右焦点坐标是(2,0),且经过点(-2,-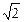 )的椭圆C的标准 方程;
)的椭圆C的标准 方程;
(2)对(1)中的椭圆C,设斜率为1的直线l交椭圆C于A、B两点,AB的中点为M,证明:当直线l平行移动时,动点M在一条过原点的定直线上;
(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
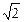 )的椭圆C的标准 方程;
)的椭圆C的标准 方程;(2)对(1)中的椭圆C,设斜率为1的直线l交椭圆C于A、B两点,AB的中点为M,证明:当直线l平行移动时,动点M在一条过原点的定直线上;
(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.

(1) 椭圆的标准方程为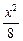 +
+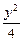 =1.
=1.
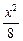 +
+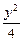 =1.
=1.(1)由题中条件,设椭圆的标准方程为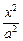 +
+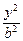 =1,a>b>0,
=1,a>b>0,
∵右焦点为(2,0),∴a2=b2+4,
即椭圆的方程为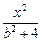 +
+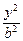 =1.
=1.
∵点(-2,-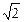 )在椭圆上,∴
)在椭圆上,∴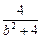 +
+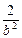 =1.
=1.
解得b2=4或b2=-2(舍),
由此得a2=8,即椭圆的标准方程为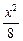 +
+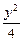 =1.
=1.
(2)设直线l的方程为y=x+m,与椭圆C的交点为A(x1,y1)、B(x2,y2),
则由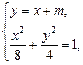 得12x2+16mx+8m2-32=0,
得12x2+16mx+8m2-32=0,
即3x2+4mx+2m2-8=0.
∵Δ>0,∴m2<12,即-2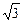 <m<2
<m<2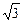 .
.
则x1+x2=- ,y1+y2=x1+m+x2+m=
,y1+y2=x1+m+x2+m=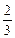 m,
m,
∴AB中点M的坐标为(-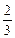 m,
m, ).
).
∴线段AB的中点M在过原点的直线x+2y=0上.
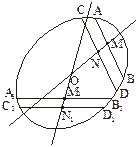
(3)如下图,作两条平行直线分别交椭圆于点A、B和点C、D,并分别取AB、CD的中点M、N,连结直线MN;又作两条平行直线(与前两条直线不平行)分别交椭圆于点A1、B1和点C1、D1,并分别取A1B1、C1D1的中点M1、N1,连结直线M1N1,那么直线MN和M1N1的交点O即为椭圆中心 .
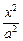 +
+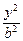 =1,a>b>0,
=1,a>b>0,∵右焦点为(2,0),∴a2=b2+4,
即椭圆的方程为
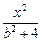 +
+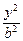 =1.
=1.∵点(-2,-
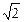 )在椭圆上,∴
)在椭圆上,∴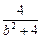 +
+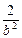 =1.
=1.解得b2=4或b2=-2(舍),
由此得a2=8,即椭圆的标准方程为
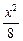 +
+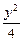 =1.
=1.(2)设直线l的方程为y=x+m,与椭圆C的交点为A(x1,y1)、B(x2,y2),
则由
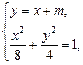 得12x2+16mx+8m2-32=0,
得12x2+16mx+8m2-32=0,即3x2+4mx+2m2-8=0.
∵Δ>0,∴m2<12,即-2
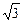 <m<2
<m<2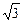 .
.则x1+x2=-
 ,y1+y2=x1+m+x2+m=
,y1+y2=x1+m+x2+m=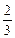 m,
m,∴AB中点M的坐标为(-
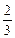 m,
m,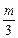 ).
).∴线段AB的中点M在过原点的直线x+2y=0上.
(3)如下图,作两条平行直线分别交椭圆于点A、B和点C、D,并分别取AB、CD的中点M、N,连结直线MN;又作两条平行直线(与前两条直线不平行)分别交椭圆于点A1、B1和点C1、D1,并分别取A1B1、C1D1的中点M1、N1,连结直线M1N1,那么直线MN和M1N1的交点O即为椭圆中心 .


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
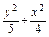 =1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
=1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.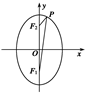
 ,-
,-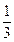 )
)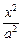 +
+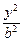 =1中心的弦,F(c,0)为椭圆的右焦点,则△AFB面积的最大值是
=1中心的弦,F(c,0)为椭圆的右焦点,则△AFB面积的最大值是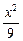 +
+ 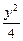 =1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是?
=1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是?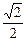 ,1)
,1) ,
, ,
,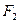 分别为其左、右焦点,
分别为其左、右焦点,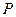 为椭圆上任意一点,
为椭圆上任意一点,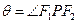 ,求
,求 的最大值及
的最大值及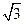 ,4+2
,4+2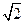 ,4+2
,4+2