题目内容
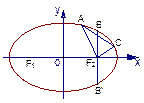
椭圆a2x2+y2=a2(0<a<1)上离顶点A(0,a)距离最远的点恰好是另一个顶点A′(0, -a),则a的取值范围是
A.(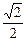 ,1) ,1) | B.[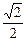 ,1) ,1) |
C.(0,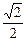 ) ) | D.(0,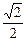 ] ] |
B
由对称性,可设P点坐标为(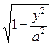 ,y),
,y),
∴|AP|2=1-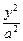 +(y-a)2
+(y-a)2
=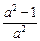 y2-2ay+a2+1.
y2-2ay+a2+1.
∵0<a<1,∴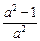 <0,开口向下.
<0,开口向下.
∴对称轴y=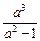 ≥-a.
≥-a.
解得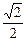 ≤a<1.
≤a<1.
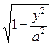 ,y),
,y),∴|AP|2=1-
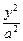 +(y-a)2
+(y-a)2=
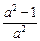 y2-2ay+a2+1.
y2-2ay+a2+1.∵0<a<1,∴
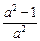 <0,开口向下.
<0,开口向下.∴对称轴y=
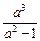 ≥-a.
≥-a.解得
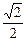 ≤a<1.
≤a<1.
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
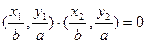 ,椭圆的离心率
,椭圆的离心率 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.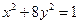 的焦点坐标是( ).
的焦点坐标是( ).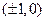
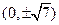
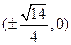
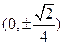
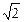 )的椭圆C的标准 方程;
)的椭圆C的标准 方程;
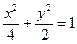 上的两个动点,
上的两个动点,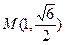 是椭圆上一定点,
是椭圆上一定点,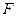 是其左焦点,且|PF|、|MF|、|QF|成等差数列。
是其左焦点,且|PF|、|MF|、|QF|成等差数列。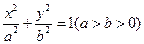 ,右焦点为
,右焦点为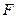 ,求连接
,求连接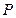 的线段
的线段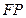 的中点
的中点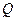 的轨迹方程.
的轨迹方程.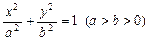 与过点A(2,0),B(0,1)的直线l有且只有一个公共点T,且椭圆的离心率
与过点A(2,0),B(0,1)的直线l有且只有一个公共点T,且椭圆的离心率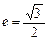 .求椭圆方程
.求椭圆方程