题目内容
AB为过椭圆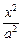 +
+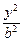 =1中心的弦,F(c,0)为椭圆的右焦点,则△AFB面积的最大值是
=1中心的弦,F(c,0)为椭圆的右焦点,则△AFB面积的最大值是
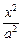 +
+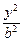 =1中心的弦,F(c,0)为椭圆的右焦点,则△AFB面积的最大值是
=1中心的弦,F(c,0)为椭圆的右焦点,则△AFB面积的最大值是| A.b2 | B.ab |
| C.ac | D.bc |
D
设A(x0,y0),B(-x0,-y0),
S△ABF=S△OFB+S△OFA=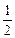 c·|y0|+
c·|y0|+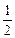 c·|-y0|=c·|y0|.
c·|-y0|=c·|y0|.
∵点A、B在椭圆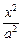 +
+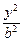 =1上,
=1上,
∴|y0|的最大值为b.
∴S△ABF的最大值为bc.
S△ABF=S△OFB+S△OFA=
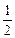 c·|y0|+
c·|y0|+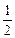 c·|-y0|=c·|y0|.
c·|-y0|=c·|y0|.∵点A、B在椭圆
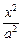 +
+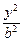 =1上,
=1上,∴|y0|的最大值为b.
∴S△ABF的最大值为bc.

练习册系列答案
相关题目
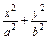 =1(a>b>0)上的三点,其中点
=1(a>b>0)上的三点,其中点 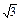 ,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.
,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.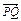 与
与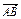 是否共线,并给出证明.
是否共线,并给出证明.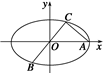
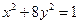 的焦点坐标是( ).
的焦点坐标是( ).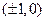
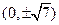
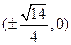
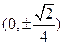
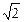 )的椭圆C的标准 方程;
)的椭圆C的标准 方程;
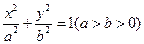 ,右焦点为
,右焦点为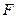 ,求连接
,求连接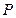 的线段
的线段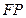 的中点
的中点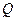 的轨迹方程.
的轨迹方程.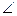 B=
B=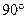 ,
,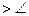 B,则以C为焦点,且以A、B为顶点的椭圆的离心率为__________;
B,则以C为焦点,且以A、B为顶点的椭圆的离心率为__________;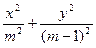 =1的准线平行于x轴,则m应满足的条件是( )
=1的准线平行于x轴,则m应满足的条件是( )