题目内容
如图所示,点P是椭圆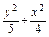 =1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
=1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.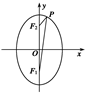
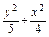 =1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
=1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
8-4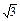
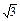
在椭圆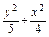 =1中,
=1中,
a=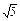 ,b=2.∴c=
,b=2.∴c=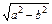 =1.
=1.
又∵点P在椭圆上,
∴|PF1|+|PF2|=2a=2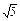 . ①
. ①
由余弦定理知:
|PF1|2+|PF2|2-2|PF1||PF2|cos30°
=|F1F2|2=(2c)2="4. " ②
①式两边平方得
|PF1|2+|PF2|2+2|PF1|·|PF2|=20, ③
③-②得(2+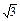 )|PF1|·|PF2|=16,
)|PF1|·|PF2|=16,
∴|PF1|·|PF2|=16(2-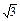 ), ∴
), ∴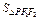 =
=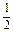 |PF1|·|PF2|sin30°=8-4
|PF1|·|PF2|sin30°=8-4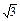 .
.
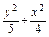 =1中,
=1中,a=
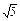 ,b=2.∴c=
,b=2.∴c=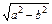 =1.
=1.又∵点P在椭圆上,
∴|PF1|+|PF2|=2a=2
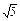 . ①
. ①由余弦定理知:
|PF1|2+|PF2|2-2|PF1||PF2|cos30°
=|F1F2|2=(2c)2="4. " ②
①式两边平方得
|PF1|2+|PF2|2+2|PF1|·|PF2|=20, ③
③-②得(2+
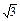 )|PF1|·|PF2|=16,
)|PF1|·|PF2|=16,∴|PF1|·|PF2|=16(2-
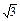 ), ∴
), ∴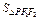 =
=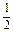 |PF1|·|PF2|sin30°=8-4
|PF1|·|PF2|sin30°=8-4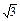 .
.
练习册系列答案
相关题目
 ,椭圆的离心率
,椭圆的离心率 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.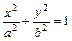 (a>b>0),动圆
(a>b>0),动圆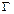 :
: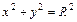 ,其中b<R<a. 若A是椭圆ε上的点,B是动圆
,其中b<R<a. 若A是椭圆ε上的点,B是动圆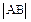 的最大值.
的最大值.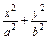 =1(a>b>0)上的三点,其中点
=1(a>b>0)上的三点,其中点 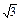 ,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.
,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.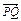 与
与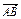 是否共线,并给出证明.
是否共线,并给出证明.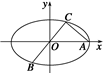
 的图象恒过定点A。若点A在直线mx+ny+1=0上,其中mn>0,当
的图象恒过定点A。若点A在直线mx+ny+1=0上,其中mn>0,当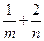 有最小值时,椭圆
有最小值时,椭圆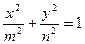 的离心率为 。
的离心率为 。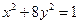 的焦点坐标是( ).
的焦点坐标是( ).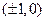
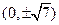
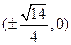
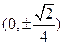
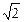 )的椭圆C的标准 方程;
)的椭圆C的标准 方程;
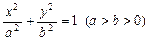 与过点A(2,0),B(0,1)的直线l有且只有一个公共点T,且椭圆的离心率
与过点A(2,0),B(0,1)的直线l有且只有一个公共点T,且椭圆的离心率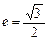 .求椭圆方程
.求椭圆方程