题目内容
(本小题满分10分).
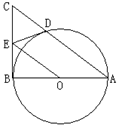
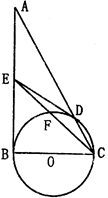
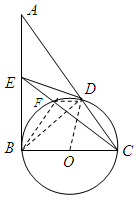
(选修4-1) 如图,在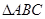 中,
中, ,以
,以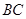 为直径的圆
为直径的圆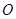 交
交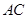 于点
于点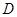 ,设
,设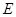 为
为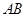 的中点.
的中点.
(I)求证:直线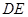 为圆
为圆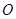 的切线;
的切线;
(Ⅱ)设 交圆
交圆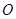 于点
于点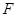 ,求证:
,求证: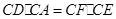
(选修4-1) 如图,在
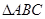 中,
中, ,以
,以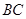 为直径的圆
为直径的圆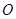 交
交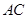 于点
于点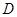 ,设
,设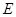 为
为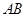 的中点.
的中点.
(I)求证:直线
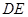 为圆
为圆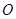 的切线;
的切线;(Ⅱ)设
 交圆
交圆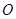 于点
于点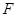 ,求证:
,求证: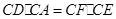
见解析。
(I)先连接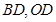 ,易知
,易知 ,进一步得到
,进一步得到 ,
,
再由等腰 中,
中, ,然后可得
,然后可得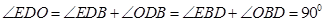 ,问题得证.
,问题得证.
(II) 证明本题的关键是证明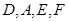 四点共圆,然后根据同旁内角互补四点共圆即可.
四点共圆,然后根据同旁内角互补四点共圆即可.
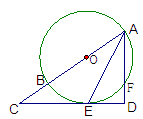
证明:(Ⅰ)连接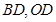
在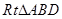 中,
中,
则有在等腰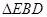 中,
中, …… 2分
…… 2分
在等腰 中,
中,
可得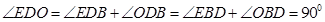
即直线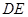 为圆
为圆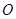 的切线 …… 5分
的切线 …… 5分
(Ⅱ)连接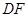 ,则有
,则有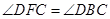 , …… 6分
, …… 6分
又因为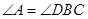 , 可得
, 可得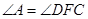 则有
则有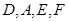 四点共圆…… 8分
四点共圆…… 8分
因此得到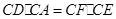 …… 10分
…… 10分
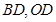 ,易知
,易知 ,进一步得到
,进一步得到 ,
,再由等腰
 中,
中, ,然后可得
,然后可得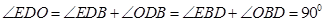 ,问题得证.
,问题得证.(II) 证明本题的关键是证明
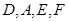 四点共圆,然后根据同旁内角互补四点共圆即可.
四点共圆,然后根据同旁内角互补四点共圆即可.
证明:(Ⅰ)连接
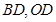
在
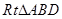 中,
中,
则有在等腰
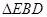 中,
中, …… 2分
…… 2分在等腰
 中,
中,
可得
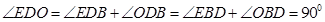
即直线
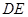 为圆
为圆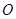 的切线 …… 5分
的切线 …… 5分(Ⅱ)连接
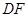 ,则有
,则有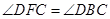 , …… 6分
, …… 6分又因为
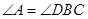 , 可得
, 可得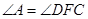 则有
则有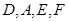 四点共圆…… 8分
四点共圆…… 8分因此得到
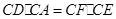 …… 10分
…… 10分
练习册系列答案
相关题目
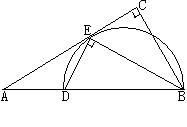
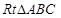 中,
中,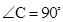 ,
,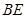 平分
平分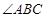 交
交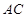 于点
于点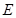 ,点
,点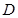 在
在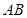 上,
上,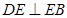 .
.
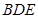 的外接圆的切线;
的外接圆的切线;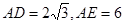 ,求
,求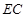 的长.
的长. 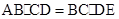
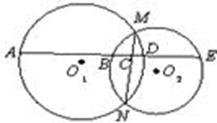
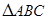 中,
中,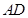 为
为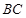 边上的中线,
边上的中线,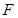 为
为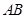 上任意一点,
上任意一点,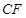 交
交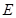 .求证:
.求证: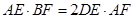 .
. 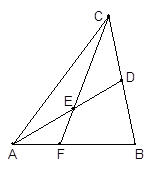
 上一点
上一点 在直径
在直径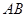 上的射影为
上的射影为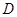 .
.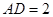 ,
,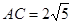 ,则
,则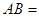 .
.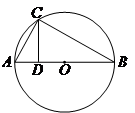
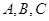 是圆
是圆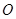 上的点,
上的点,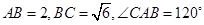 ,则
,则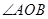 对应的劣弧长为 .
对应的劣弧长为 .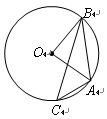
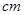 和18
和18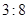 ,则另一弦的
,则另一弦的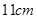
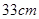
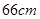
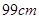
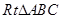 的直角边
的直角边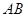 为直径作圆
为直径作圆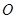 ,圆
,圆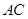 交于
交于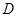 ,过
,过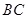 交于
交于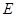 ,若
,若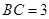 ,
,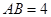 ,则
,则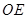 ="_________"
="_________"