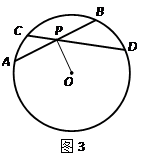题目内容
. 以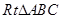 的直角边
的直角边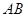 为直径作圆
为直径作圆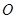 ,圆
,圆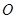 与斜边
与斜边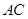 交于
交于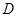 ,过
,过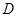 作圆
作圆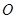 的切线与
的切线与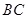 交于
交于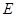 ,若
,若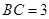 ,
,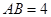 ,则
,则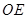 ="_________"
="_________" 
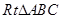 的直角边
的直角边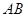 为直径作圆
为直径作圆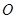 ,圆
,圆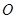 与斜边
与斜边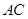 交于
交于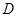 ,过
,过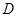 作圆
作圆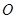 的切线与
的切线与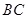 交于
交于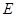 ,若
,若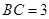 ,
,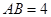 ,则
,则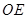 ="_________"
="_________" 
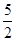
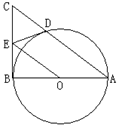
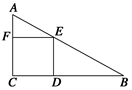
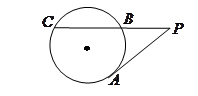
解:由题意,连接OD,BD,则OD⊥ED,BD⊥AD
∵OB=OD,OE="OE" ∴Rt△EBO≌Rt△EDO
∴EB=ED,∴∠EBD=∠EDB
又∠EBD+∠C=90°,∠EDB+∠EDC=90°
∴∠C=∠EDC,∴ED=EC
∴EB=EC
∵O是AB的中点,∴OE=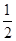 AC
AC
∵直角边BC=3,AB=4,
∴AC=5
∴OE=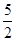
故答案为: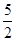
∵OB=OD,OE="OE" ∴Rt△EBO≌Rt△EDO
∴EB=ED,∴∠EBD=∠EDB
又∠EBD+∠C=90°,∠EDB+∠EDC=90°
∴∠C=∠EDC,∴ED=EC
∴EB=EC
∵O是AB的中点,∴OE=
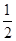 AC
AC∵直角边BC=3,AB=4,
∴AC=5
∴OE=
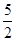
故答案为:
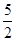

练习册系列答案
相关题目
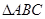 中,
中, ,以
,以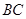 为直径的圆
为直径的圆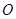 交
交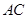 于点
于点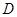 ,设
,设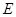 为
为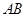 的中点.
的中点.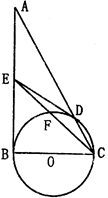
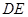 为圆
为圆 交圆
交圆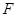 ,求证:
,求证: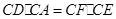
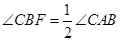 .
.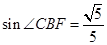 ,求BC和BF的长.
,求BC和BF的长.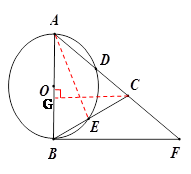
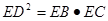
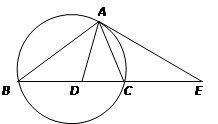
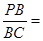
 ,
,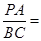
 1
1 点在圆
点在圆 直径
直径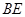 的延长线上,
的延长线上,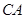 切圆
切圆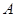 点,
点,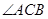 的平分线
的平分线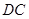 交
交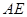 于点
于点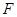 ,交
,交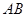 于
于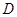 点.
点.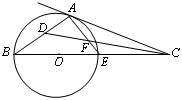
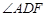 的度数;
的度数;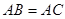 时,求证:
时,求证: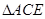 ∽
∽ ,并求相似比
,并求相似比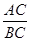 的值.
的值.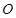 的半径为
的半径为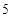
 ,点
,点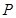 是弦
是弦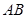 的中点,
的中点,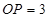
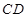 过点
过点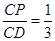 ,则
,则