题目内容
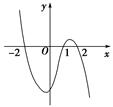
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )

| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(-2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(-2) |
| D.函数f(x)有极大值f(-2)和极小值f(2) |
D
当x<-2时,y=(1-x)f′(x)>0,
得f′(x)>0;
当-2<x<1时,y=(1-x)f′(x)<0,得f′(x)<0;
当1<x<2时,y=(1-x)f′(x)>0,得f′(x)<0;
当x>2时,y=(1-x)f′(x)<0,得f′(x)>0,
∴f(x)在(-∞,-2)上是增函数,在(-2,1)上是减函数,在(1,2)上是减函数,在(2,+∞)上是增函数,
∴函数f(x)有极大值f(-2)和极小值f(2).
得f′(x)>0;
当-2<x<1时,y=(1-x)f′(x)<0,得f′(x)<0;
当1<x<2时,y=(1-x)f′(x)>0,得f′(x)<0;
当x>2时,y=(1-x)f′(x)<0,得f′(x)>0,
∴f(x)在(-∞,-2)上是增函数,在(-2,1)上是减函数,在(1,2)上是减函数,在(2,+∞)上是增函数,
∴函数f(x)有极大值f(-2)和极小值f(2).

练习册系列答案
相关题目
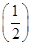 1-x,则:
1-x,则: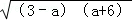 (﹣6≤a≤3)的最大值为( )
(﹣6≤a≤3)的最大值为( )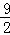
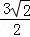
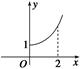
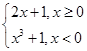
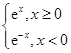
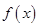 是定义在R上的偶函数,且
是定义在R上的偶函数,且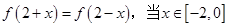 时,
时,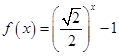 ,若在区间
,若在区间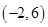 内,函数
内,函数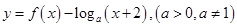 恰有1个零点,则实数
恰有1个零点,则实数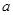 的取值范围是( )
的取值范围是( )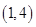
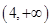
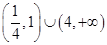
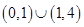
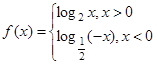 ,若
,若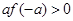 ,则实数
,则实数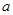 的取值范围是( )
的取值范围是( )
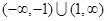
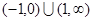
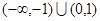
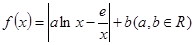 且
且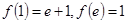 ,求函数
,求函数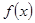 的单调区间.
的单调区间.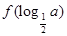 ≤2f(1),则a的取值范围是 ( )
≤2f(1),则a的取值范围是 ( )