题目内容
函数f(x)的定义域为R，f(－1)＝2，对任意x∈R，f′(x)>2，则f(x)>2x＋4的解集为( )
| A．(－1,1) | B．(－1，＋∞) |
| C．(－∞，－1) | D．(－∞，＋∞) |
B
f′(x)>2转化为f′(x)－2>0，
构造函数F(x)＝f(x)－2x，
得F(x)在R上是增函数．
又F(－1)＝f(－1)－2×(－1)＝4，f(x)>2x＋4，
即F(x)>4＝F(－1)，所以x>－1．
构造函数F(x)＝f(x)－2x，
得F(x)在R上是增函数．
又F(－1)＝f(－1)－2×(－1)＝4，f(x)>2x＋4，
即F(x)>4＝F(－1)，所以x>－1．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
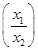＝f(x1)－f(x2)，且当x>1时，f(x)<0.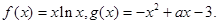
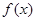的最小值；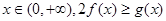
恒成立，求实数
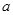的取值范围．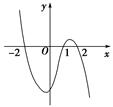
（
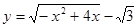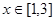）的图象绕坐标原点逆时针旋转
（
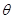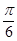
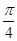
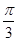
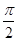
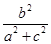的最大值为 ．
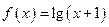，若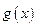
是以2为周期的偶函数，且当
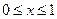时，有
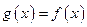，则函数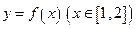
的反函数为（ ）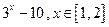
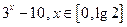
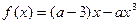在区间[0,1]上的最小值等于-3，则实数
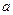的取值范围是 ( )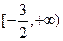
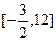
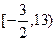
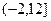
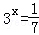，则（ ）