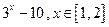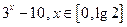题目内容
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+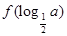 ≤2f(1),则a的取值范围是 ( )
≤2f(1),则a的取值范围是 ( )
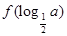 ≤2f(1),则a的取值范围是 ( )
≤2f(1),则a的取值范围是 ( )| A.[1,2] |
B.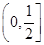 |
C.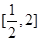 |
| D.(0,2] |
C
由题意知a>0,又 =log2a-1=-log2a.
=log2a-1=-log2a.
∵f(x)是R上的偶函数,
∴f(log2a)=f(-log2a)=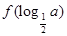 .
.
∵f(log2a)+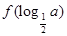 ≤2f(1),
≤2f(1),
∴2f(log2a)≤2f(1),即f(log2a)≤f(1).又因f(x)在[0,+∞)上递增.
∴|log2a|≤1,-1≤log2a≤1,
∴a∈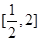 ,选C
,选C
 =log2a-1=-log2a.
=log2a-1=-log2a.∵f(x)是R上的偶函数,
∴f(log2a)=f(-log2a)=
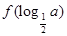 .
.∵f(log2a)+
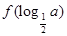 ≤2f(1),
≤2f(1),∴2f(log2a)≤2f(1),即f(log2a)≤f(1).又因f(x)在[0,+∞)上递增.
∴|log2a|≤1,-1≤log2a≤1,
∴a∈
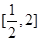 ,选C
,选C
练习册系列答案
相关题目
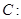
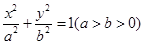 的左焦点为
的左焦点为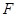 ,左、右顶点分别为
,左、右顶点分别为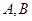 ,过点
,过点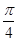 的直线
的直线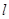 交椭圆于
交椭圆于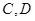 两点,椭圆
两点,椭圆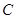 的离心率为
的离心率为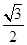 ,
,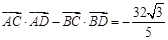 .
.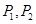 是椭圆上不同两点,
是椭圆上不同两点,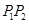
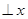 轴,圆
轴,圆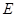 过点
过点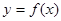 的定义域为
的定义域为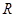 ,若存在常数
,若存在常数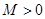 ,使得
,使得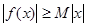 对一切实数
对一切实数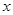 均成立,则称
均成立,则称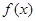 为“圆锥托底型”函数.
为“圆锥托底型”函数.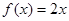 ,
,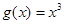 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由. 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出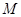 的最大值.
的最大值.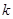 、
、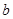 满足什么条件,
满足什么条件,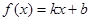 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.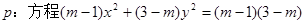 表示的曲线是双曲线;命题
表示的曲线是双曲线;命题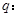 函数
函数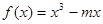 在区间
在区间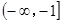 上为增函数,若“
上为增函数,若“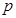
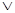
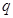 ”为真命题,“
”为真命题,“
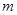 的取值范围.
的取值范围.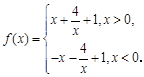
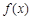 的奇偶性;
的奇偶性;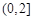 和
和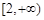 上的增减性;
上的增减性;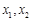 满足:
满足: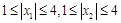 ,试证明:
,试证明: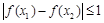 .
.
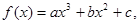 其导函数
其导函数 的图象如图,则函数
的图象如图,则函数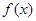 的极小值是( )
的极小值是( )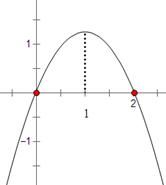


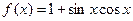 ,则函数
,则函数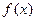 的单调递减区间为( )
的单调递减区间为( )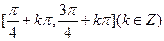
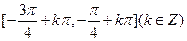
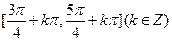
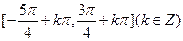
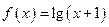 ,若
,若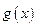 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当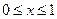 时,有
时,有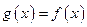 ,则函数
,则函数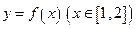 的反函数为( )
的反函数为( )