题目内容
17.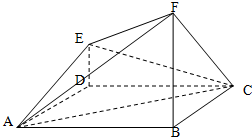 一个多面体如图所示,四边形ABCD是边长为2的正方形,AB=FB,FB⊥平面ABCD,ED∥FB,且ED=1.
一个多面体如图所示,四边形ABCD是边长为2的正方形,AB=FB,FB⊥平面ABCD,ED∥FB,且ED=1.(1)求证:平面ACE⊥平面ACF.
(2)求多面体AED-BCF的体积.
分析 (1)证明OE⊥平面ACF,即可证明平面ACE⊥平面ACF.
(2)多面体ADE-BCF的体积V=${V_{E-ACD}}+{V_{F-ABC}}+V_{E-ACF}^{\;}$,分别求出体积,即可求多面体AED-BCF的体积.
解答 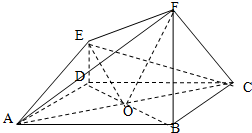 (1)证明:连接BD,AC与BD交于点O,连接OE,OF.
(1)证明:连接BD,AC与BD交于点O,连接OE,OF.
∵四边形ABCD是四边形ABCD是正方形,FB⊥平面ABCD,ED∥FB
∴DE⊥平面ABCD,AE=CE,OE⊥AC ①
又∵DE=1,CD=2,
则OE=$\sqrt{3}$,OF=$\sqrt{6}$,EF=3
∴OE2+OF2=EF2,则OE⊥OF ②
由①,②得,OE⊥平面ACF,
∴平面ACF⊥ACE;
(2)解:由(1)可知,三棱锥E-ACD,三棱锥F-ABC的高分别是DE,BF.且AC⊥平面BDEF,
故多面体ADE-BCF的体积V=${V_{E-ACD}}+{V_{F-ABC}}+V_{E-ACF}^{\;}$
而${V_{E-ACD}}=\frac{2}{3}$,${V_{F-ABC}}=\frac{4}{3}$,$V_{E-ACF}^{\;}$=2
∴多面体ADE-BCF的体积V=4.
点评 本题考查了面面垂直的判定,考查了用分割法求多面体的体积,考查了学生的空间想象能力与推理论证能力.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
7.i10=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
8.已知f(x)=$\left\{\begin{array}{l}{(1-2a)x+3a,}&{x<1}\\{lnx,}&{x≥1}\end{array}\right.$的值域为R,那么a的取值范围是( )
| A. | (-∞,-1] | B. | (-1,$\frac{1}{2}$) | C. | [-1,$\frac{1}{2}$) | D. | (0,$\frac{1}{2}$) |
12.sin33°•sin63°+cos63°•sin57°的值等于( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
2.设集合A={x|x=π+$\frac{2kπ}{3}$,k∈z},B={x|x=kπ+$\frac{π}{3}$,k∈z},C={x|x=kπ+$\frac{2π}{3}$,k∈z},则A∩(B∪C)=( )
| A. | $\left\{{x|x=kπ+\frac{π}{3},k∈z}\right\}$ | B. | $\left\{{x|x=kπ-\frac{π}{3},k∈z}\right\}$ | C. | $\left\{{x|x=2kπ±\frac{π}{3},k∈z}\right\}$ | D. | $\left\{{x|x=kπ±\frac{π}{3},k∈z}\right\}$ |
9.复数z=$\frac{1-i}{2+i}$(i为虚数单位)的虚部为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$i |
6.已知A,B均为锐角,sinA=$\frac{{\sqrt{5}}}{5}$,sinB=$\frac{{\sqrt{10}}}{10}$,则A+B的值为( )
| A. | $\frac{7π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$ |