题目内容
4.已知点M(1,-1),N(-1,1),则以线段MN为直径的圆的方程是( )| A. | x2+y2=$\sqrt{2}$ | B. | x2+y2=1 | C. | x2+y2=4 | D. | x2+y2=2 |
分析 根据中点坐标公式算出MN的中点坐标为(0,0),且|MN|=2$\sqrt{2}$,从而得到所求圆的圆心为原点、半径r=$\sqrt{2}$,可得圆的标准方程.
解答 解:∵点M(1,-1),N(-1,1),
∴线段MN的中点坐标为(0,0),且|MN|=2$\sqrt{2}$.
因此,以线段MN为直径的圆,它的圆心为(0,0),半径r=$\frac{1}{2}$|MN|=$\sqrt{2}$,
∴圆的方程为x2+y2=2.
故选:D.
点评 本题给出M、N两点的坐标,求以AB为直径的圆的方程.着重考查了线段中点坐标公式、两点间的距离公式和圆的标准方程等知识,属于基础题.

练习册系列答案
相关题目
19.直线y=x-2与圆x2+y2-4x+3=0交于A、B两点,与抛物线y2=8x交于C、D两点,则|AB|+|CD|=( )
| A. | 16 | B. | 14 | C. | 18 | D. | $14\sqrt{2}$ |
9.若m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A. | α∥β,m?α,n?β⇒m∥n | B. | α⊥β,n∥α,m⊥β⇒n⊥m | C. | m∥n,m∥α⇒n∥α | D. | m∥n,m⊥α⇒n⊥α |
14.设集合A={x|2x+1<3x},B={x|-3<x<2},则A∩B等于( )
| A. | {x|-3<x<1} | B. | {x|1<x<2} | C. | {x|x>-3} | D. | {x|x<1} |
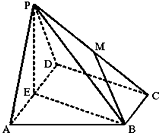 如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,PA=PD=4,BC=$\frac{1}{2}$AD=2,CD=2$\sqrt{3}$.
如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,PA=PD=4,BC=$\frac{1}{2}$AD=2,CD=2$\sqrt{3}$.