题目内容
12.在锐角△ABC中,已知内角A、B、C所对的边分别为a、b、c,且$\sqrt{3}$(tanA-tanB)=1+tanA•tanB,a2-ab=c2-b2,求A、B、C的大小.分析 根据两角和差的正切公式以及余弦定理分别进行求解即可.
解答 解:∵$\sqrt{3}$(tanA-tanB)=1+tanA•tanB.
∴tan(A-B)=$\frac{tanA-tanB}{1+tanAtanB}$=$\frac{\sqrt{3}}{3}$,
即A-B=$\frac{π}{6}$,
∵a2-ab=c2-b2,
∴a2+b2-c2=ab,
即cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{ab}{2ab}=\frac{1}{2}$,
∴C=$\frac{π}{3}$,
即A+B=$\frac{2π}{3}$,
∵A-B=$\frac{π}{6}$,
∴A=$\frac{5π}{12}$,B=$\frac{π}{4}$.
点评 本题主要考查解三角形的应用,根据余弦定理以及两角和差的正切公式进行化简是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列表述正确的是( )
①归纳推理是由部分到整体的推理;
②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理;
④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理.
①归纳推理是由部分到整体的推理;
②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理;
④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理.
| A. | ①②③ | B. | ②③④ | C. | ①③⑤ | D. | ②④⑤ |
20.某程序框图如图所示,则输出的结果为( )
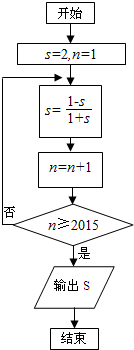

| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | -3 |
4.已知点M(1,-1),N(-1,1),则以线段MN为直径的圆的方程是( )
| A. | x2+y2=$\sqrt{2}$ | B. | x2+y2=1 | C. | x2+y2=4 | D. | x2+y2=2 |