题目内容
15.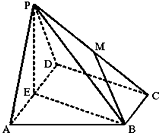 如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,PA=PD=4,BC=12AD=2,CD=2√3.
如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,PA=PD=4,BC=12AD=2,CD=2√3.(Ⅰ)求证:PA⊥CD;
(Ⅱ) 若M是棱PC的中点,求直线PB与平面BEM所成角的正弦值;
(Ⅲ)在棱PC上是否存在点N,使二面角N-EB-C的余弦值为√1313,若存在,确定点N的位置;若不存在,请说明理由.
分析 (Ⅰ)证明PE⊥面ABCD,利用PA在面ABCD内的射影是CD,CD⊥AD,即可证明:PA⊥CD;
(Ⅱ)建立空间直角坐标系,求出→PB,平面BEM的一个法向量,利用向量的夹角公式求直线PB与平面BEM所成角的正弦值;
(Ⅲ)设→PN=λ→PC(0≤λ≤1),求出平面NEB的一个法向量,利用向量的夹角公式,结合二面角N-EB-C的余弦值为√1313,即可得出结论.
解答 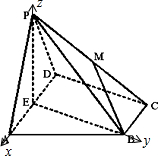 解:(Ⅰ)∵等腰△PAD中,E为AD的中点,∴PE⊥AD.
解:(Ⅰ)∵等腰△PAD中,E为AD的中点,∴PE⊥AD.
∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,
∴PE⊥面ABCD,
又PA在面ABCD内的射影是CD,CD⊥AD,
由三垂线定理知:CD⊥PA;…(4分)
(Ⅱ)以E为原点,分别以→EA,→EB,→EP的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,
由PE=4cos30°=2√3得P(0,0,2√3)
又∵C(-2,2√3,0),
∴M(-1,√3,√3),
∴→EM=(-1,√3,√3),
又→EB=(0,2√3,0)
设平面BEM的一个法向量为→n=(x,y,z),
则{2√3y=0−x+√3y+√3z=0,
令z=1则x=√3,y=0,
∴→n=(√3,0,1),
又∵→PB=(0,2√3,-2√3),
设直线PB与平面BEM所成角为θ,
则sinθ=|−2√3|2×√24=√24; …(8分)
(3)假设在棱PC上存在点N,使二面角N-EB-C的余弦值为√1313,
设→PN=λ→PC(0≤λ≤1),则→EN=(-2λ,2√3λ,2√3(1-λ)),
又→EB=(0,2√3,0),设平面NEB的一个法向量为→m=(a,b,c),
则\left\{\begin{array}{l}{2\sqrt{3}b=0}\\{-2λa+2\sqrt{3}λb+2\sqrt{3}(1-λ)c=0}\end{array}\right.,
令c=λ,a=\sqrt{3}(1-λ),
∴\overrightarrow{m}=(\sqrt{3}(1-λ),0,λ),
又\overrightarrow{m′}=(0,0,1)为平面EBC的一个法向量,
则cos<\overrightarrow{m},\overrightarrow{m′}>=\frac{|λ|}{\sqrt{3(1-λ)^{2}+{λ}^{2}}}=\frac{\sqrt{13}}{13},解得λ=\frac{1}{3}(负值舍),
故存在点N为棱PC的靠近P的三分点符合条件.…(12分)
点评 本题主要考查线面垂直的判定,以及二面角的求解,建立空间坐标系,利用向量法是解决二面角的常用方法.考查学生的运算和推理能力.

①归纳推理是由部分到整体的推理;
②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理;
④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理.
| A. | ①②③ | B. | ②③④ | C. | ①③⑤ | D. | ②④⑤ |
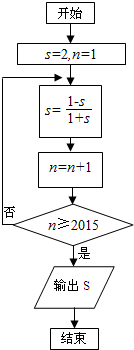
| A. | \frac{1}{2} | B. | 2 | C. | -\frac{1}{3} | D. | -3 |
| A. | x2+y2=\sqrt{2} | B. | x2+y2=1 | C. | x2+y2=4 | D. | x2+y2=2 |