题目内容
直线x+y=a 与圆x2+y2=1交于不同的两点A,B,O为坐标原点,若
•
=a,则a的值为( )
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与圆相交的性质
专题:直线与圆
分析:联立方程得到方程组,消元得到2x2-2ax+a2-3=0,由韦达定理得x1x2,y1y2的值,再由
•
=a,代入可求解.
 |
| OA |
 |
| OB |
解答:
解:联立直线x+y=a与圆x2+y2=1,消掉y并整理得:2x2-2ax+a2-1=0,
设A(x1,y1),B(x2,y2),则由韦达定理得:
x1+x2=a,x1x2=
,
∴y1y2=(a-x1)(a-x2)=a2-a(x1+x2)+x1x2 =a2-a2+x1x2=
.
又
•
=a,∴x1x2+y1y2=a,代入可得a2-a-1=0,解得a=
或a=
.
由题意可得
•
∈[-1,1],∴a=
,
故选:B.
设A(x1,y1),B(x2,y2),则由韦达定理得:
x1+x2=a,x1x2=
| a2-1 |
| 2 |
∴y1y2=(a-x1)(a-x2)=a2-a(x1+x2)+x1x2 =a2-a2+x1x2=
| a2-1 |
| 2 |
又
| OA |
| OB |
1-
| ||
| 2 |
1+
| ||
| 2 |
由题意可得
| OA |
| OB |
1-
| ||
| 2 |
故选:B.
点评:本题考查直线与圆的位置关系,注意韦达定理及整体思想的运用,属基础题.

练习册系列答案
相关题目
(文)现有四个函数:①y=x•sinx;②y=x•cosx;③y=x|cosx|;④y=x•2x的图象(部分)如图:

则按照从左到右图象对应的函数序号安排正确的一组是( )

则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |
{an}为等比数列,Sn是其前n项和,若a2•a3=8a1,且a4与2a5的等差中项为20,则S5=( )
| A、29 | B、30 | C、31 | D、32 |
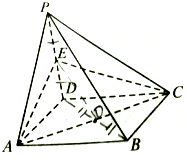 如图,四棱锥P-ABCD的侧面PAD是正三角形,且垂直于底面,底面ABCD是矩形,E是PD的中点,求证:平面ACE⊥平面PCD.
如图,四棱锥P-ABCD的侧面PAD是正三角形,且垂直于底面,底面ABCD是矩形,E是PD的中点,求证:平面ACE⊥平面PCD.