题目内容
【题目】已知椭圆 
的左焦点为F，C与过原点的直线相交于A，B两点，连接AF、BF，若|AB|=10，|AF|=6，cos∠ABF= 
，则C的离心率e= ．
【答案】
【解析】解：设椭圆的右焦点为F'，连接AF'、BF'
∵AB与FF'互相平分，∴四边形AFBF'为平行四边形，可得|AF|=|BF'|=6
∵△ABF中，|AB|=10，|AF|=6，cos∠ABF= 
，
∴由余弦定理|AF|2=|AB|2+|BF|2﹣2|AB|×|BF|cos∠ABF，
可得62=102+|BF|2﹣2×10×|BF|× ，解之得|BF|=8
由此可得，2a=|BF|+|BF'|=14，得a=7
∵△ABF中，|AF|2+|BF|2=100=|AB|2
∴∠AFB=90°，可得|OF|= 
|AB|=5，即c=5
因此，椭圆C的离心率e= 
=
所以答案是： 
练习册系列答案
相关题目
【题目】为了更好地规划进货的数量，保证蔬菜的新鲜程度，某蔬菜商店从某一年的销售数据中，随机抽取了8组数据作为研究对象，如表所示（
（吨）为买进蔬菜的数量，
（天）为销售天数）：
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（1）根据上表数据在所给坐标系中绘制散点图，并用最小二乘法求出关于的线性回归方程
；
（2）根据（Ⅰ）中的计算结果，该蔬菜商店准备一次性买进25吨，预计需要销售多少天？
（参考数据和公式：
，
，
，
，
，
.）
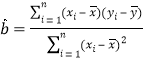
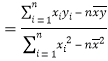