Question

【题目】设等差数列{an}的前n项和为Sn ， 且S4=4S2 ， a2n=2an+1．
（1）求数列{an}的通项公式；
（2）设数列{bn}的前n项和为Tn且 （λ为常数）．令cn=b2n（n∈N*）求数列{cn}的前n项和Rn ．

Answer 1

【答案】
（1）解：设等差数列{an}的首项为a1，公差为d，由a2n=2an+1，取n=1，得a2=2a1+1，即a1﹣d+1=0①

再由S4=4S2，得 ，即d=2a1②

联立①、②得a1=1，d=2．

所以an=a1+（n﹣1）d=1+2（n﹣1）=2n﹣1

（2）解：把an=2n﹣1代入 ，得 ，则 ．

所以b1=T1=λ﹣1，

当n≥2时， = ．

所以 ， ．

Rn=c1+c2+…+cn= ③

④

③﹣④得： =

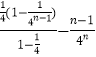
所以 ；

所以数列{cn}的前n项和

【解析】（1）设出等差数列的首项和公差，由已知条件列关于首项和公差的方程组，解出首项和公差后可得数列{an}的通项公式；（2）把{an}的通项公式代入 ，求出当n≥2时的通项公式，然后由cn=b2n得数列{cn}的通项公式，最后利用错位相减法求其前n项和．
【考点精析】本题主要考查了等差数列的通项公式（及其变式）和数列的前n项和的相关知识点，需要掌握通项公式：或；数列{an}的前n项和sn与通项an的关系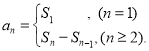才能正确解答此题．