题目内容
【题目】已知函数 ,函数
,函数![]() 有四个不同的零点,从小到大依次为
有四个不同的零点,从小到大依次为![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:通过f(x)的单调性,画出f(x)的图象和直线y=a,考虑四个交点的情况,得到x1=-2-x2,-1<x2≤0,x3x4=4,再由二次函数的单调性,可得所求范围.
详解:当x>0时,f(x)=![]() ,
,
可得f(x)在x>2递增,在0<x<2处递减,
由f(x)=e(x+1)2,x≤0,
x<-1时,f(x)递减;-1<x<0时,f(x)递增,
可得x=-1处取得极小值1,
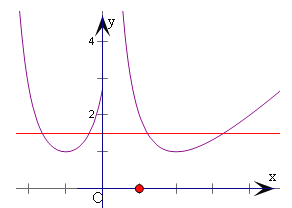
作出f(x)的图象,以及直线y=a,
可得e(x1+1)2=e(x2+1)2=![]() ,
,
即有x1+1+x2+1=0,可得x1=-2-x2,-1<x2≤0,
![]()
可得x3x4=4,
x1x2+x3x4=4-2x2-x22=-(x2+1)2+5,在-1<x2≤0递减,
可得所求范围为[4,5).
故选B.

练习册系列答案
相关题目


